Зависимости экономических переменных

Функциональная, статистическая и корреляционная

Любая экономическая политика заключается в регулировании определенных экономических показателей. Однако стратегия регулирования может быть весьма неэффективной и рискованной без достаточного знания того, как эти показатели связаны с другими переменными, часто имеющими ключевое значение для принимающего решение политика или предпринимателя. Кроме того, воздействие на многие экономические показатели не может осуществляться непосредственно. Например, нельзя непосредственно регулировать темп инфляции, но на него можно воздействовать средствами фискальной (бюджетно-налоговой) и монетарной (кредитно-денежной) политики. Поэтому, в частности, должна быть изучена зависимость между предложением денег и уровнем цен.

В реальных экономических ситуациях даже устоявшиеся зависимости могут проявляться неоднозначно. Еще более сложной проблемой является анализ малоизученных и нестабильных зависимостей, построение моделей которых является основной задачей современной эконометрики. Разработка эффективных эконометрических моделей невозможна без проведения на всех этапах исследований качественного и количественного анализа с использованием реальных статистических данных. Основными инструментами таких исследований являются методы корреляционного и регрессионного анализа. Модели регрессионного анализа занимают центральное место в математическом аппарате эконометрики.

В естественных науках обычно имеют дело со строгой (функциональной) зависимостью, при которой каждому значению одной переменной соответствует единственное значение другой. В экономике в большинстве случаев имеют место зависимости, когда каждому значению одной переменной соответствует определенное (условное) распределение другой. Такую зависимость называют статистической (вероятностной). В частности, статистическая зависимость может проявляться в том, что при изменении одной из величин изменяется среднее значение (условное математическое ожидание) другой. В этом случае статистическая зависимость называется корреляционной. Так, например, при рассмотрении взаимосвязи между двумя переменными Х и Y может быть представлена усредненная по Х схема зависимости, где условное математическое ожидание М_х(Y) изменяется в зависимости от Х = х.

Односторонняя зависимость, выражаемая соотношением

М_х(Y) = φ(x), (2.1)

называется функцией регрессии или просто регрессией Y на Х. При этом зависимую переменную Y называют также функцией отклика, результативным признаком или результирующей переменной, а независимую переменную Х – регрессором, фактором-аргументом, факторным признаком. Соотношение (2.1), определяющее взаимосвязь между двумя переменными, представляет собой парную регрессию. Зависимость нескольких экономических переменных, выражаемую уравнением:

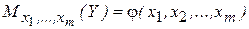, (2.2)

называют множественной (многомерной) регрессией.

Термин «регрессия» (движение назад, возвращение в прежнее состояние) был введен Френсисом Галтоном в конце XIX в. при анализе зависимости между ростом родителей и ростом детей. Галтон установил, что рост детей у высоких родителей меньше, чем средний рост родителей. У низких родителей, наоборот, средний рост детей выше. И в том, и в другом случае средний рост детей стремится (возвращается) к среднему росту людей в данном регионе. Сущность такой зависимости отражается используемым термином.

В настоящее время основными задачами регрессионного анализа являются установление формы зависимости между СВ, оценка функции регрессии, оценка неизвестных значений (прогноз значений) зависимой переменной.