Основные предпосылки МНК. Теорема Гаусса-Маркова

Доказано (доказательство можно найти в [2]), что для получения по МНК наилучших результатов (для эффективного применения МНК) необходимо, чтобы выполнялся ряд предпосылок относительно случайного отклонения ε_i.

1. Математическое ожидание случайного отклонения равно нулю: М(ε_i) = 0 для всех наблюдений.

Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. В каждом конкретном наблюдении отклонение ε_i может быть либо положительным, либо отрицательным, но не должно иметь систематического смещения. Отметим, что выполнимость этой предпосылки определяет равенство математического ожидания зависимой переменной y_i линейной функции регрессии: М(y_i) = b₀ + b₁x_i.

2. Дисперсия случайных отклонений ε_i постоянна для любых наблюдений: D(ε_i)=σ².

Поскольку 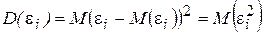, то данную предпосылку можно записать в виде .

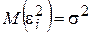Данное условие подразумевает, что несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть либо большим, либо меньшим, не должно быть некоторой априорной причины, вызывающей увеличение ошибки, т. е. увеличение случайного отклонения.

Выполнимость данной предпосылки называется гомоскедастичностью, а невыполнимость ее – гетероскедастичностью (непостоянством дисперсии отклонений).

На практике гетероскедастичность довольно часто возникает, если анализируемые объекты неоднородны по своим экономическим характеристикам. Например, если исследуется зависимость прибыли предприятий от размеров основных фондов, то естественно ожидать, что для больших предприятий колебания прибыли будут выше, чем для малых.

3. Случайные отклонения ε_i и ε_j являются независимыми друг от друга для i ¹ j.

Другими словами, случайные отклонения (ошибки) в любых различных наблюдениях некоррелированы, т. е. отсутствует систематическая связь между любыми случайными отклонениями.

Данное условие предполагает выполнимость следующего соотношения:

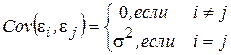. (2.14)

Условие некоррелированности ошибок часто нарушается, если наши статистические данные являются временными рядами. В этом случае мы имеем модель с автокорреляцией случайных отклонений.

Искажающие эффекты, связанные с гетероскедастичностью и автокорреляцией случайных отклонений (остатков, ошибок), будут рассмотрены более подробно в главе 5.

4. Случайные отклонения ε_i имеют нормальное распределение.

Выполнимость данной предпосылки необходима для оценки точности уравнения регрессионной модели и его параметров с использованием схемы проверки статистических гипотез и построения интервальных оценок.

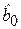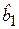Теорема Гаусса-Маркова. Если регрессионная модель удовлетворяет предпосылкам 1-4 (условиям Гаусса-Маркова), то оценки параметров и , полученные по МНК, являются несмещенными, состоятельными и эффективными; т. е. они имеют наименьшие дисперсии среди всех возможных линейных оценок данных параметров.

При выполнении предпосылок Гаусса-Маркова и условия, что х_i является неслучайной (детерминированной) величиной, парная модель y_i = b₀ + b₁x_i + ε_i будет называться классической линейной регрессионной моделью.