Парная линейная регрессия

Под уравнением регрессии будем понимать функциональную зависимость между объясняющими переменными и условным математическим ожиданием (средним значением) зависимой переменной, которая строится с целью определения оценки этого среднего значения.

Если функция регрессии линейна, то говорят о линейной регрессии, и общее теоретическое уравнение парной регрессии имеет вид:

М_х(Y) = b₀ + b_1x. (2.3)

Для отражения того факта, что реальные значения зависимой переменной Y не всегда совпадают с ее условными математическими ожиданиями, следует ввести в соотношение (2.3) случайное слагаемое (случайное отклонение) ε:

Y = M_x(Y) + ε = b₀ + b₁ + ε, (2.4)

которое по существу является СВ и указывает на вероятностный характер зависимости.

Соотношение (2.4) представляет теоретическую линейную регрессионную модель (модель парной линейной регрессии) в общем виде. Тогда для каждого индивидуального значения (наблюдения) y_i будем иметь:

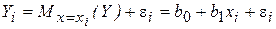. (2.5)

Индивидуальные значения y_i представлены в виде двух компонент – систематической, объясняемой уравнением регрессии b₀ + b₁x_i, и случайной (необъясненной) – ε_i.

По реальным наблюдениям (по выборке ограниченного объема) мы сможем построить так называемое эмпирическое уравнение регрессии.

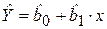, (2.6)

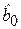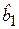где Ŷ -оценка условного математического ожидания М_х(Y), и - оценки неизвестных теоретических параметров модели b₀ и b₁, называемые эмпирическими коэффициентами регрессии. Следовательно, для конкретных значений y_i в случае эмпирической парной модели справедливо следующее соотношение:

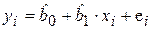, (2.7)

где отклонение (остаток) e_i представляет собой оценку теоретического случайного отклонения ε_i.

Линейная регрессионная модель является наиболее распространенным и удобным для анализа видом зависимости между экономическими переменными. Простейшее парное уравнение позволяет достаточно наглядно (часто с помощью графической интерпретации) рассмотреть основные приемы регрессионного анализа. Кроме того, парная регрессия может служить начальной точкой эконометрического моделирования. Например, это может быть линейная зависимость спроса на некоторый товар или услугу от цены или зависимость частного потребления от располагаемого дохода (модель Дж. Кейнса) и т. д.