Линейная модель парной регрессии. Метод наименьших квадратов (МНК). Свойство оценок МНК.
Линейная регрессия находит широкое применение в эконометрике в виде чёткой экономической интерпретации её параметров.
Линейная регрессия сводится к нахождению уравнения вида 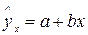 (1) или
(1) или 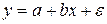 (2). Уравнение (1) позволяет по заданным значениям фактора х иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х.Уравнение (2) рассматривает укак зависимую переменную, состоящую из двух составляющих:
(2). Уравнение (1) позволяет по заданным значениям фактора х иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х.Уравнение (2) рассматривает укак зависимую переменную, состоящую из двух составляющих:
1) неслучайную составляющую 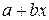 , где
, где 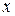 выступает как объясняющая (независимая) переменная, а
выступает как объясняющая (независимая) переменная, а 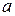 и
и 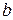 - параметры уравнения;
- параметры уравнения;
2) случайного члена - 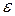 (возмущение)
(возмущение)
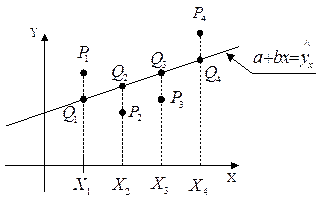
| x | x1 | x2 | x3 | x4 |
| y | y1 | y2 | y3 | y4 |
Если 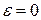 , то получатся точки
, то получатся точки 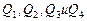 .
.
Если 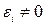 , то получим точки
, то получим точки 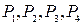
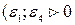
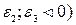 .
.
Случайный член существует по ряду причин:
1) невключение объясняющих переменных (есть ещё другие факторы, влияющие на у), но измерить их невозможно (например, психологические);
2) агрегирование переменных (объединение некоторого числа микроэкономического соотношения);
3) неправильное описание структуры модели (временные ряды зависят не только от t, но и от t-1);
4) неправильная функциональная спецификация (не линейная, а какая-то другая);
5) ошибки измерения.
εi = сумма всех этих факторов.
Рассмотрим задачу определения параметров модели, то есть коэффициентов 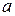 и
и 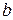 - оценке параметров модели.
- оценке параметров модели.
Оценки параметров линейной регрессии могут быть найдены разными методами, например можно построить поле корреляции, взять 2 точки и провести через них прямую.

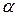 оценка параметра
оценка параметра 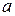 , то есть отрезок отсекаемой прямой на оси
, то есть отрезок отсекаемой прямой на оси 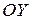 ;
;
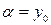 ,
, 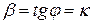 - угловой коэффициент прямой,
- угловой коэффициент прямой,
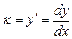 - оценка параметра
- оценка параметра 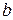 .
.
Необходимо с самого начала признать, что мы не сможем рассчитать истинные значения 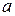 и
и 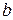 . Мы можем получить только оценки, и они могут быть или хорошими или плохими. Построение линии регрессии на глаз является достаточно субъективным.
. Мы можем получить только оценки, и они могут быть или хорошими или плохими. Построение линии регрессии на глаз является достаточно субъективным.
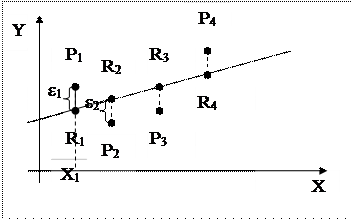
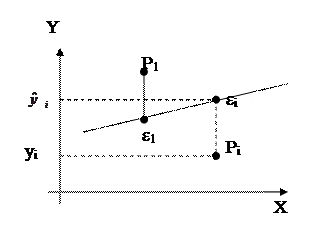
Отрезок 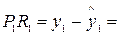 ε1 (остаток),
ε1 (остаток), 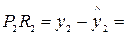 ε2. Остатки должны быть min.
ε2. Остатки должны быть min. 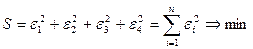 .
.
Существует целый ряд критериев:
1. МНК 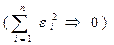 min суммы квадратов отклонений.
min суммы квадратов отклонений.
2. Минимизируется 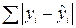 сумма модулей отклонений.
сумма модулей отклонений.
3. Функция Хубера 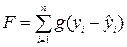 , где
, где 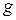 - «мера» с которой отклонение входит в функционал.
- «мера» с которой отклонение входит в функционал.
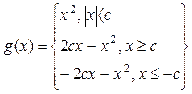

Рассмотрим достоинства и недостатки перечисленных функционалов.
1) сумма квадратов отклонений:
«+» лёгкость вычисления, хорошие статистические свойства, простота математических выводов делают возможным построить развитую теорию, позволяющую провести тщательную проверку различных статистических гипотез;
«-» чувствительность к выбросам;
2) сумма модулей отклонений:
«+» робастость, то есть нечувствительность к выбросам;
«-» сложность вычислительной процедуры, большим отклонениям надо придавать больший вес (лучше 2 отклонения по 1, чем одно 0 и 2), неоднозначность, то есть разным значениям параметра 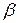 могут соответствовать одинаковые суммы модулей отклонений.
могут соответствовать одинаковые суммы модулей отклонений.
Функция Хубера является попыткой совместить достоинства двух первых функционалов.
Рассмотрим МНК:
Из множества линий регрессии на графике выбирается та, сумма квадратов отклонений была минимальной.
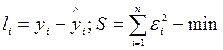
Чтобы найти min надо взять частные производные по 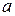 и
и 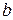 функции S и приравнять их нулю.
функции S и приравнять их нулю.
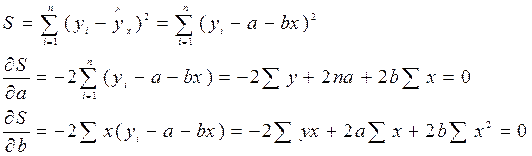
Получим систему нормальных уравнений для оценки параметров a и b. (3)
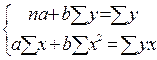 (3)
(3)
Решая систему (3) любым методом: исключение, Крамера (через определители), найдем оценки параметров a и b. МНК даёт самые точные несмещённые и эффективные оценки 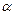 и
и 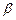 .
.
Можно воспользоваться формулами: если 1 уравнение системы (3)
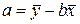
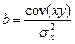
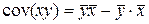 - ковариация признаков;
- ковариация признаков;
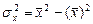 - дисперсия признака х.
- дисперсия признака х.
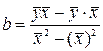
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата (у) с изменением фактора х на одну единицу. Зависимость между расходами на питание (у) и располагаемым личным доходом (х) за период 1959 по 1983 г. В США описывается уравнением регрессии.
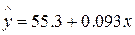 , х увеличился на 1 единицу, а у на 0,093ед.
, х увеличился на 1 единицу, а у на 0,093ед.
Х увеличился на 1 млрд $, то у (расходы на питание) возрастут на 93 млн $ (т. е. из 1 $ дохода 9,3 цента – на питание).
 Параметр а,
Параметр а, 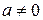 . Уравнение регрессии теряет смысл, «а» - не имеет экономического содержания. Интерпретировать можно только знак при параметре а.
. Уравнение регрессии теряет смысл, «а» - не имеет экономического содержания. Интерпретировать можно только знак при параметре а. 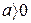 - относительное изменение параметра у, происходит медленнее, чем изменение фактора или вариации результата.
- относительное изменение параметра у, происходит медленнее, чем изменение фактора или вариации результата.
Коэффициенты вариации 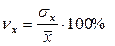 ;
; 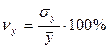 ;
;
Если 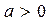 , то
, то 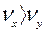 ;
;
Если 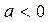 , то
, то 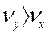
Возможность чёткой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в экономических исследованиях.
Дата добавления: 2016-05-16; просмотров: 1828;
