Свойства выборочных вариаций (дисперсий) и ковариаций.

Для дальнейшего изложения нам понадобится установить ряд пра­вил, которые можно использовать при преобразовании выражений, со­держащих выборочные вариации и ковариации.

Пусть а — некоторая постоянная, а х, у, z — переменные, прини­мающие в i-м наблюдении значения x_i,y_i,z_i,i=1,..., п (n — количество наблюдений). Тогда а можно рассматривать как переменную, значение которой в i-м наблюдении равно а, и

Соv(х, а) =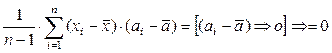

откуда следует свойство:

1. Cov(x, a) = 0.

Далее, нетрудно видеть, что имеют место равенства:

2. Cov(x, у) = Cov(y, х);

3. Cov(x, x) = Var(x).

Кроме того,

Cov(ax, y) = =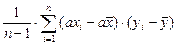

откуда следует свойство:

4. Cov(ax. у) = aCov(x, у).

Далее, имеем

Cov(xy,z) = =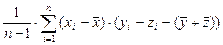

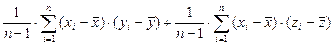
так что можно сформулировать еще одно свойство:

5. Cov(x. у + z) =Cov(x, у) + Cov(x,z).

На основе вышеназванных свойств находим, что

6. Var(a)=0 ,

т. е. постоянная не обладает изменчивостью и

7. Var(ax)=a²Var(x).

Таким образом, при изменении единицы измерения переменной в раз, во столько же раз преобразуется и величина стандартного отклоне­ния этой переменной (напомним, что стандартное отклонение равно квадратному корню из дисперсии).

8. Var(x+a)=Var(x)

т. е. сдвиг начала отсчета не влияет на вариацию переменной.

Далее, имеем:

Var(x+y)=Cov(x+y,x+y)= Cov(x, х) + Cov(x, у) + Cov(y, x) + Cov(x, у).

Таким образом, доказано свойство

9.Var(x+y)=Var(x)+Var(y)+2Cov(x,y),

означающее, что вариация суммы двух переменных отличается от сум­мы вариаций этих переменных на величину, которая равна удвоенному значению ковариации между названными переменными.

Свойства остатков

Теперь установим почти очевидные соотношения, которые следуют из условии минимума критерия наименьших квадратов. Определим величину

ŷ_i=a +bx,

— оценку переменной у при оптимальных значениях коэффициентов регрессии и фиксированном значении х в i-ом наблюдении. Такую оценку называют прогнозом зависимой переменной. Тогда, очевидно, ошибка модели в i-ом наблюдении будет равна ε_i=y_i - ŷ_i и из условия следует, что

т. е сумма квадратов ошибок оценок переменной у (остатков модели) при оптимальных параметрах регрессии а и b равна нулю.

Далее, вытекает, что

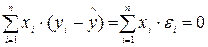
т. е., при оптимальных параметрах регрессии ошибки ортогональны на­блюдениям независимой переменной.