Статистические свойства оценок метода наименьших квадратов.

Поскольку полученные оценки a и b коэффициентов линейной рег­рессии опираются на статистические данные и являются случайными величинами, то естественно установить свойства названных оценок; как случайных величин. Более того, не выяснив этих свойств, невоз­можно сделать обоснованные выводы относительно качества и надеж­ности полученных оценок. Необходимо, в частности, определить такие их статистические характеристики, как математическое ожидание и дисперсия. К желательным свойствам оценок относятся также несмещенность и состоятельность. Далее, если бы удалось установить вид распределения (плотности распределения) оценок, можно было бы по­строить доверительные интервалы для истинных значений параметров регрессии (т. е. получить интервальные оценки коэффициентов) и реа­лизовать процедуры проверки гипотез относительно их значений. Важ­ную роль играет также изучение статистических свойств остатков оце­ненной регрессии.

Все эти задачи можно решить, основываясь на некоторых правдопо­добных теоретических предпосылках (гипотезах) модели, выполнение которых на практике подлежит проверке с помощью специально разра­ботанных для этого статистических процедур.

Основные предпосылки РА ( ε_i – случайная величина, x_i – неслучайная величина):

Предположение относительно независимых переменных

В дальнейшем будем допускать, что х — детерминированная (не­случайная) величина, т. е. значения независимых переменных заранее известны. Данное предположение (предпосылка), к сожалению, на практике при моделировании реальных социально-экономических процессов часто не выполняется. Это связано с тем, что здесь в качест­ве независимых переменных часто выступают стохастические некон­тролируемые величины, такие как интенсивность потока покупателей (в одном из примеров главы 1) или рыночный индекс в рыночной мо­дели, который также является случайной величиной. При нарушении вышеупомянутой предпосылки ряд «хороших» свойств оценок сохра­няется (при некоторых условиях), но в отдельных случаях требуется корректировка модели (оценок).

Предположения относительно случайной составляющей модели

При выполнении предпосылки относительно переменной х стати­стические свойства оценок параметров и зависимой переменной, а так­же, остатков, целиком определяются вероятностными свойствами случайной составляющей регрессионной модели. Относительно слу­чайной составляющей в классическом регрессионном анализе предпо­лагают выполнение следующих условий, которые называются условия­ми Гаусса-Марковаи играют ключевую роль при изучении свойств оце­нок, полученных по методу наименьших квадратов:

1. Первое условие заключается в том, что математическое ожидание случайной составляющей во всех наблюдениях должно быть равно нулю. Формально это записывается так

М{ε_t} = 0, для всех t = 1,2,...,п.

Смысл этого условия заключается в том, что не должно быть систе­матического смещения случайной составляющей. В линейной регрес­сии систематическое смещение линии регрессии учитывается с помо­щью введения параметра смещения ε_i и поэтому данное условие можно считать всегда выполненным.

2.Дисперсия случайной составляющей постоянна для всех наблю­дений (т. е. не зависит от номера наблюдения). Это условие записыва­ется так:

D{ε_t}=M{ε_t²}=σ²,

где дисперсия σ² — величина постоянная.

Это свойство дисперсии ошибок называется гомоскедастичностью (однородностью) (запомните этот термин).

Выполнение условия гомоскедастичности при построении конкрет­ных эконометрических моделей необходимо проверять с помощью спе­циальных статистических процедур. Поскольку истинные дисперсии ошибок неизвестны, их можно лишь приближенно оценить на основе наблюдаемых (точнее, вычисляемых) значений остатков модели в каж­дом наблюдении. Таким образом, и свойство гомоскедастичности на практике проверяется (диагностируется) на самом деле для остатков мо­дели, а не для истинных ошибок, и может выполняться лишь прибли­женно. Если условие гомоскедастичности не выполнено (т. е. дисперсия ошибок не постоянна), то говорят, что имеет место условие гетероскедастичности (запомните этот термин). Понятия «гомоскедастичность» и «гетероскедастичность» являются ключевыми в эконометрике.

Графическая иллюстрация понятий «гомоскедастичность» и «гетероскедастичность»

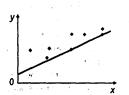
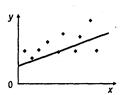
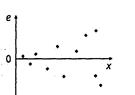
Рис. 2.6а

Гомоскедастичность Рис.2.6б Рис. 2.6в

Гетероскедастичность Гетероскедастичные остатки

3. Случайные составляющие модели для различных наблюдений некоррелированы. Это условие записывается таким образом:

М{εi, εj}=0, для всех i≠j (i, j=1,2,…,n)

Выполнение данного условия означает отсутствие систематической (статистической) связи между значениями случайного члена в любых двух наблюдениях. Это свойство на практике также проверяется с по­мощью статистических процедур на основе анализа остатков модели.

Если оно нарушается, то процедура оценки параметров должна быть скорректирована.

4. Четвертое условие Гаусса-Маркова записывается так:

M{x_I, εj}=0, для всех i и j,

и означает, что объясняющие переменные и случайные составляющие некоррелированы для всех наблюдений. Ранее мы предположили, что объясняющая переменная в модели не является стохастической. В этом случае четвертое условие выполняется автоматически.

Регрессионная модель с детерминированными регрессорами, удовлетво­ряющая предпосылкам Гаусса-Маркова, называется классической регрес­сионной моделью.