Эффективность (оптимальность) оценок

До сих пор мы говорили об оптимальности оценок в смысле мини­мума квадратичного критерия. Оказывается, что при выполнении условий Гаусса-Маркова они являются также оптимальными в смысле минимума дисперсии.

Оценка называется эффективной, если она имеет минимальную дис­персию по сравнению с другими оценками заданного класса.

Таким образом, оценки наименьших квадратов являются эффек­тивными, т. е. наилучшими в смысле минимума диспепсии, в классе всех линейных несмещенных оценок параметров.

Рассмотрим функции плотности вероятности и одиночного наблюдения и выборочного среднего.

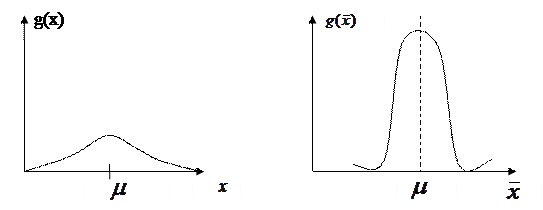
Величина х считается распределённой. Распределения и симметрично относительно 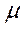-теоретического среднего. Разница в том, что распределение - уже и выше. Величина , ближе к 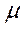, чем значение единичного наблюдения, поскольку её случайная составляющая 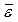, есть среднее от чисто случайных составляющих 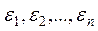в выборке и они как-бы «гасят» друг друга при расчёте среднего.

Вычтем из (1) (2):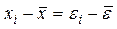

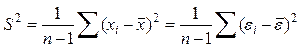, то есть оценка теоретической дисперсии 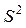зависит от (и только от) числа случайной составляющей наблюдений х в выборке. Поскольку эти составляющие меняются от выборки к выборке, так от выборки к выборке меняется и величина оценки .

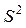Несмещённость.

Поскольку оценки являются случайными переменными, их значения лишь по случайному совпадению могут в точности равняться характеристикам генеральной совокупности. Обычно будет присутствовать определённая ошибка, которая может быть большой, или малой, положительной или отрицательной, в зависимости от чисто случайных составляющих величин х в выборке.

Желательно, чтобы оценка в среднем за достаточно длительный период была аккуратной. То есть математическое ожидание оценки = соответствующей характеристике генеральной совокупности. Такая оценка называется несмещённой. Если это не так, то оценка называется смещённой и разница, между её М. О. и соответствующей теоретической характеристикой генеральной совокупности называется смещением.

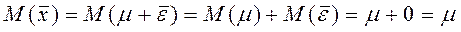
Полученная оценка – не единственно возможная несмещённая оценка . Рассмотрим выборку из всего двух наблюдений и . Любое взвешенное среднее наблюдений и 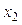было бы несмещённой оценкой, если сумма весов равна 1. Докажем, это. Рассмотрим обобщённую форму оценки:

,

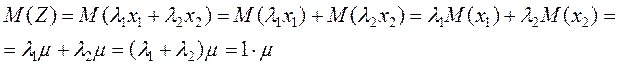то ,

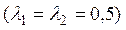
z – несмещенная оценка.

Эффективность.

Несмещённость – желательное свойство оценок, но не единственное свойство. Ещё одна их важная сторона – это надёжность. Конечно, немаловажно, чтобы оценка была точной в среднем за длительный период. Пусть имеем две оценки теоретического среднего, рассчитанных на основе одной и той же информации. Поскольку функция плотности вероятности для В более «сжата», чем для А, с её помощью мы скорее получим более точное значение. Таким образом оценка В более эффективна. Эффективна та оценка, дисперсия которой min.