Дополнительное предположение о нормальном распределении ошибок

При выполнении условий Гаусса-Маркова, оценки наименьших квадратов обладают такими свойствами, как несмещенность, состоя­тельность и оптимальность (эффективность). Однако, для построения доверительных интервалов и проверки гипотез относительно истинных значений параметров, необходимо дополнительное предположение о распределении случайной составляющей ε_i. В классическом регресси­онном анализе допускается, что эта составляющая распределена по нормальному закону и тогда модель называют классической нормальной линейной регрессией. (1-4) достаточно, а 5 необходимо для оценки точности уравнения регрессии.

Данное предположение является, пожалуй, наиболее спорным. Дело в том, что предположение о нормальности можно считать правдо­подобным, если значения случайной величины порождаются в резуль­тате воздействия большого количества независимых случайных факто­ров, каждый из которых не обязательно имеет нормальное распределе­ние. Примером такого воздействия является так называемое броуновское движение (хаотичное движение малых частиц в жидкости как результат совокупного воздействия на частицу — ударов, соударе­ния — большого количества молекул жидкости).

В экономических процессах распределения случайных величин, как правило, отличаются от нормального, поскольку механизм их по­рождения более сложный. Тем не менее, чаще всего именно нормаль­ное распределение используется в эконометрических исследованиях (как, впрочем, и в статистике). Это обусловлено следующими причинами. Во-первых, нормальный закон действительно часто достаточно хорошо (с приемлемой для практики точностью) аппроксимирует (приближенно описывает) распределение случайной составляющей. Во-вторых, что очень важно, на основе нормального распределения можно получить процедуры проверки гипотез и построения доверительных интервалов, удобные для расчетов и применения на практи­ке. В любом случае, не изучив базовые результаты (процедуры), осно­ванные на предположении нормальности, нельзя продвигаться на бо­лее высокий уровень изучения и применения более реалистичных моделей, не использующих эту предпосылку и позволяющих получать более точные результаты.

Замечание. Если случайные величины в модели распределены по нормальному закону, то из свойств некоррелированности в третьем и четвертом условиях Гаусса-Маркова следует и независимость соответ­ствующих случайных величин.

Оценкой модели является уравнение:

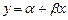
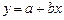
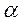а - оценка они определяются МНК

b - оценка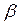

Несмещенная оценка остаточной дисперсии учитывает воздействие факторов и ошибок неучтенных в модели, определяется с помощью дисперсии возмущения (ошибок) или остаточной дисперсии σ2, - это выборочная остаточная дисперсия.

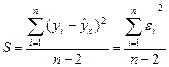
Являются ли оценки a, b и s² наилучшими выясняется по условиям Гаусса-Маркова: если регрессионная модель удовлетворяет предпосылкам 1-4, то оценки a и b имеют наименьшую дисперсию в классе линейных несмещенных оценок.