Уравнение регрессии, его смысл и назначение. Выбор типа математической функции при построении уравнения регрессии.

Регрессионный анализ- это процесс определения аналитического выражения функции связи, в котором изменение результативной или зависимой переменной происходит под влиянием факторной или независимой переменной. Построение модели парной регрессии позволяет количественно оценить взаимосвязь между результативной и факторной переменной.

В парной регрессии выбор вида математической функции 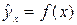может быть осуществлён тремя методами:

- графическим;

- аналитическим;

Экспериментальным.

Графический метод достаточно нагляден. Он основан на поле корреляции. Основные типы кривых, используемые при количественной оценке связей:

а) линейная; б) квадратичная; в) гипербола;

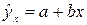
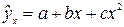
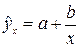
г) кубическая; д) степенная; е) показательная;

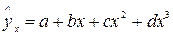
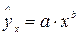
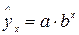
Ещё может быть:

; ; ;

; ; ;

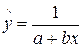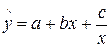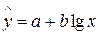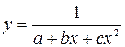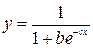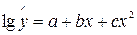Аналитический методоснован на изучении материальной природы связи исследуемых признаков.

Пусть изучается потребность предприятия в электроэнергии y в зависимости от объёма выпускаемой продукции. Выделим две части:

- не связанная с производством продукции а;

- непосредственно связанная с объёмом выпускаемой продукции bx.

Тогда: 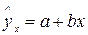если обе части уравнения поделить почленно на x, то получим выражение зависимости удельного расхода электроэнергии на единицу продукции 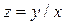от объёма выпущенной продукции, 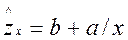(равносторонняя гипербола).

Затраты:

- условно-переменные, изменяющиеся пропорционально изменению объёма продукции (расход материала, оплата труда);

- условно-постоянные, не зависящие от объёма продукции (арендная плата, содержание администрации и др.).

Зависимость затрат на производство y от объёма продукции x, характеризуется линейной функцией 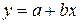, зависимость себестоимости единицы продукции z от объёма .

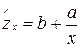При обработке информации на компьютере выбор УР осуществляется экспериментально, путём сравнения остаточной дисперсии (Д_ост) при разных моделях. Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при 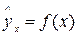, фактическое значение результата признака совпадает с теоретическим 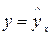. Д_ост=0, то есть обусловлено влиянием только х. На практике наблюдается рассеивание точек относительно линии регрессии

.

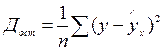Если дисперсии равны, то предпочтение отдаётся долее простым видам функции. Число наблюдений в 6-7 раз должно превышать число рассчитываемых параметров.

После того, как модель специфицирована (т. е. определен вид функ­циональной зависимости между переменными), для полного построе­ния регрессионной модели необходимо решить следующие, по сути, математико-статистические, проблемы:

I) оценить параметры модели по имеющимся наблюдаемым данным зависимой и независимых переменных;

2) провести статистический анализ полученных оценок, изучить их свойства, установить степень их надежности;

3) провести статистический анализ модели в целом и таким образом установить степень адекватности созданной модели имеющимся стати­стическим данным или, иными словами, проанализировать уровень доверия к построенной модели;

4) оценить прогнозные возможности модели, степень надежности и достоверности прогнозов, т. е. насколько правильно модель объясняет поведение изучаемого объекта.

Без решения вышеперечисленных проблем задача построения моде­ли не может считаться полностью завершенной. Для решения каждой из них в эконометрической теории в настоящее время разработано множество различных методов и подходов, основные из которых и яв­ляются предметом исследования в дальнейшем. Здесь же заострим вни­мание на роли информационного обеспечения моделей. Необходимо четко представлять, что никакие, даже самые изощренные математиче­ские методы, не заменят достоверной, постоянно обновляемой стати­стической информации об изучаемом объекте или процессе. Полно­ценное информационное наполнение модели — основа успеха при эко­нометрическом моделировании. Нельзя получать достоверные выводы, опираясь на недостоверную информацию.

Поэтому сбор и оценка качества статистических данных являются, вполне вероятно, самыми важными этапами построения эконометри­ческой модели. Необходимо также хорошо представлять, насколько достоверными являются имеющиеся данные. Если нельзя получить другие, более качественные данные, скажем, из-за высокой стоимости дополнительных статистических исследований, или недоступности ка­чественной информации, нужно правильно оценить принципиальную возможность построения адекватной модели на основе таких данных, в том числе используя формально-математические методы. Надо четко представлять границы применимости таких моделей. Именно для по­нимания и правильного решения этих проблем следует основательно изучать курс «Эконометрика». Специалист, владеющий эконометрическими методами, получает преимущество и на рынке труда и при веде­нии собственного бизнеса.