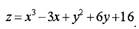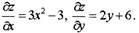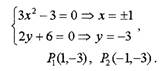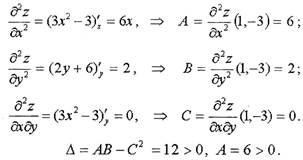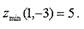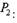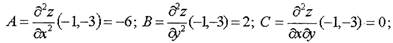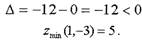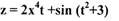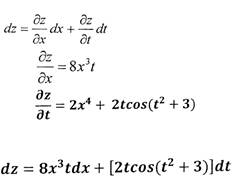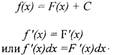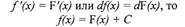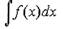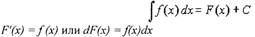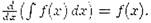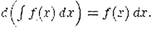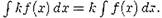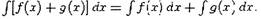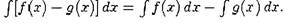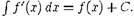3 страница. График возрастающей функции показан на рисунке 1(a).
График возрастающей функции
показан на рисунке 1(a).
Если из неравенства х2 > х1
вытекает нестрогое неравенство f (х2)
>f(х1), то функция f(х) называется
неубывающей в интервале (a, b ).
Пример такой функции показан на
рисунке 2(a).
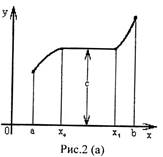
На интервале [ х0, х1 ] она сохраняет
постоянное значение С
Определение 2.
Функция f (х) называется убывающей
в интервале (а, b ) если при
возрастании аргумента х в этом
интервале соответствующие
значения функции f(x) убывают, т.е. если
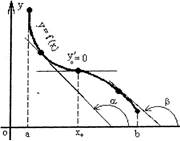 Рис.1 (б)
Рис.1 (б)
|
f(x2) <f(x1) при x2 > x1.
| вытекает нестрогое неравенство
|
функции показан на рисунке 2(б). На интервале постоянное значение С.
|
| Теорема 1 .Дифференцируемая и возрастающая в интервале ( a, b ) функция f (х) имеет во всех точках этого интервала неотрицательную производную.
|
| Доказательство. Так как функция
|
| интервала одинаковы. Следовательно
|
| положительна или равна нулю в интервале
|
| положительная величина может стремиться или к положительному числу или к нулю (смотри рисунок 1 (а)).
Очевидно, теорема 1 имеет место и для неубывающей в интервале (a, b) функции (смотри рисунок 2(a)).
|
| Из этого определения следует, что у убывающей в интервале ( а, b ) функции f (х) в любой точке этого интервала приращения Δх и Δу имеют разные знаки.
|
График убывающей функции показан на рисунке 1(б).
называется невозрастающей в интервале
отношение
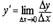
|
Теорема 2. Дифференцируемая и убывающая в интервале ( a, b ) функция
f (х) имеет во всех точках этого интервала неположительную производную.
Доказательство. Так как функция f(х) убывает в интервале (а, b ), то в
любой точке этого интервала знаки у приращений Δх и Δу различны'. Поэтому
имеет отрицательный знак, а следовательно и производная
или имеет отрицательный знак, или обращается в нуль, так как
как отрицательная величина, может стремиться или к

Значение f(x0) функции f(x), при
котором выполняется вышеуказанное
неравенство, называется максимальным
значением функции f(x) или просто
максимумом.
Определение 3.
Максимумом функции f (х) называется такое значение f(х0) этой функции,
которое не меньше всех значений функции f (х) в точках х, достаточно
близких к точке х0 , т.е. в точках х, принадлежащих некоторой достаточно
малой окрестности точки х0 .
Так, на рисунке 3 показаны два максимума: f (х0) и f(х2) .
В той точке, где функция переходит от убывания к возрастанию, ордината
меньше ординат в достаточно близких к ней точках, расположенных справа и
слева от нее. Так ордината точки В меньше ординат в точках соседних и
достаточно близких к точке х, справа и слева. Значение функции в точке,
абсцисса которой равна x1 меньше значений функции в точках, абсциссы
которых достаточно мало отличаются от х1 :
f(x1)<f(x1+Δx).
На рисунке 4(б) изображена функция f (х), непрерывная в интервале ( a, b ).
В интервале (а, х0 ] она убывает, на интервале [ х0, x1 ] - сохраняет
постоянное значение: f (х0) = f(x1) = С, в интервале [ x1, b ) - возрастает. Во
всех точках, достаточно близких к х0 (или x1 ), значения функции f (х)
удовлетворяют нестрогому неравенству
f(x1) ≤ f(x).
Значение f(х0) функции f(х), при котором выполняется вышеуказанное
неравенство, называется минимальным значением функции f(х) или просто
минимумом.
Определение 4.
Минимумом функции f(х) называется такое значение f (х0) этой функции,
которое не больше всех значений функции f(х) в точках х, достаточно
близких к точке х0 , т.е. в точках х, принадлежащих некоторой достаточно
малой окрестности точки х0 .
Так, на рисунке 3 показаны два минимума: f(х1) и f(х3) .
По определению наибольшим значением функции f(х) на интервале [a, b]
является такое значение f (х0), для которого для всех точек интервала [ a, b ]
выполняется неравенство f (х0)≥f (х), а наименьшим значением функции f(х)
на интервале [a, b ] является такое значение f (х0), для которого для всех
точек интервала [ a, b ] выполняется неравенство f(x0)<f (х).
Из этих определений следует, что функция может достигать своего
наибольшего или наименьшего значения как внутри интервала [ a, b ] , так и
на его концах а и b. Здесь же максимум и минимум функции f(х) были
определены соответственно как наибольшее и наименьшее значения в
некоторой окрестности точки х().
Если в точке х0 функция f(х) достигает максимума или минимума, то
говорят, что функция f(х) в точке х0 достигает экстремума (или
экстремального значения).
Функция f(х) может иметь несколько экстремумов внутри интервала [ a, b ],
причем может оказаться, что какой-нибудь минимум будет больше какого-
нибудь максимума. Таким образом, наибольшее значение функции f(х) на
интервале [ a, b ] - это наибольший из экстремумов функции внутри этого
интервала и наибольшее из значений функции на концах интервала.
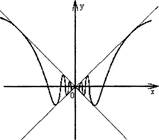 Рис. 5
Рис. 5
|
Аналогично наименьшее значение функции f (х) на интервале [ a, b ] - это
наименьший из экстремумов функции внутри этого интервала и наименьшее
из значений функции на концах интервала.
Например функция, изображенная на
рисунке 3, достигает наибольшего значения
f (х) в точке х2 , наименьшего - в точке x1
интервала [х(), x3 ]. На рисунке 5
изображена функция, имеющая
бесконечное число минимумов и
максимумов.
Теорема 3 (необходимый признак
экстремума). Если функция f (х) имеет в
точке x0 экстремум, то ее производная в
данной точке или равна нулю или не
существует.
Доказательство. Пусть в точке х0 функция f (х) дифференцируема и
достигает максимума (рисунок 3 и рисунок 4(a)). Это значит, что при
достаточно малом h > 0 как f (х0 + h) ≤ f (х0), так и f (x0 - h) < f (x0).
Из этих неравенств следует, что
Отсюда
а потому
и в то же время
Аналогично доказывается первое утверждение теоремы 3 и в том случае,
когда функция f(х) достигает в точке х0 минимума.
Но функция f(х) может иметь экстремумы и в тех точках x0 в которых ее
производная не существует. Например, функция у = | х | в точке х0 = 0 не
дифференцируема, но достигает минимума. Точки такого типа называют
угловыми. В них кривая не имеет определенной касательной.
 Рис. 6
Рис. 6
|
Таким образом, необходимым
признаком существования в точке х0
экстремума функции f (х) является выполнение следующего условия: в точке
x0 производная f (х) или равна нулю, или не существует.
Этот признак не является достаточным условием существования
экстремума функции f(х) в точке х0 : можно привести много примеров
функций, удовлетворяющих этому условию при х = х0 , но, однако, не
достигающих экстремума при x= х0.
Например, производная функции y = х3 при х0 = 0 равна нулю, однако эта
функция при x0 = 0 не достигает экстремального значения.
Тренинг: решение примеров
Пример Найдите производную функции
Пример Найдите производную функции
Решение:
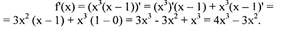
|
Пример Найдите производную функции
Решение:
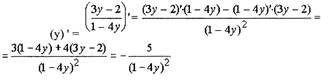
|
Решение:
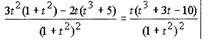
|
| Пример. Найдите производную функции
|
Пример.
Найти производную функции
Решение.
Преобразуем квадратный корень в степень: Данная функция - сложная, используем последовательно формулы: производная степенной функции, производная дроби, производная логарифма.
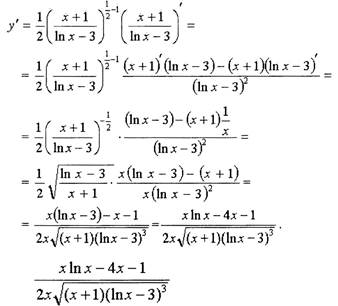 Ответ:
Ответ:
|
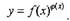 функцию:
функцию:
|
Пример.
Вычислить производную функции
Решение.
Данная функция относится к виду показательно - степенной функции
Для нахождения ее производной прологарифмируем данную
Дифференцируя левую и правую часть этого равенства, получаем
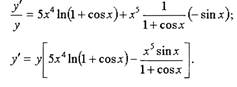
|
Пример
| функции, заданной неявно,
|
Вычислить производную
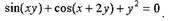
|
Решение.
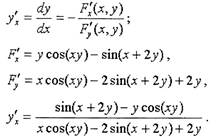
|
Ответ:
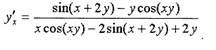
|
Пример.
Вычислить производную y'x функции, заданной параметрически:
Решение.
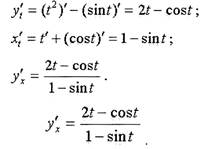 Ответ:
Ответ:
|
Пример.
Найти наибольшее и наименьшее значение функции
отрезке [ 1; 3] .
Решение.
Наибольшее и наименьшее значение на отрезке функция может достигать:
1) на концах отрезка (т.е. при х = 1 или х = 3 );
| В данном случае критическая точка
|
| левым концом, поэтому достаточно найти y (1), у (3) и выбрать из них наибольшее и наименьшее значение.
|
| 2) в критических точках, если они существуют и принадлежат [ 1; 3]. Найдем критические точки. Для этого найдем у' и решим уравнение у'= 0.
|
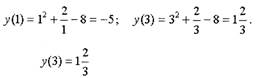 Ответ:
наименьшее значение функции.
Ответ:
наименьшее значение функции.
|
Пример Найти приближённое приращение функции у = 4х2 +5х +21, если х =
10; Δх = 1
Пример При измерении стороны квадрата относительная погрешность
| - наибольшее значение функции;
|
| , используя формулу приближенных
|
| Вычислить приближенно вычислений.
|
Решение.
Воспользуемся формулой приближенных вычислений:
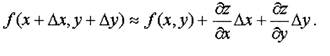
|
составила 1%. Определите относительную погрешность
измерения площади в этом случае.
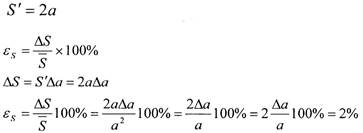 Пример
Пример
|
| , заменив числовые значения
|
переменными. Полагаем
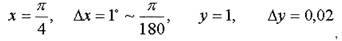
|
тогда
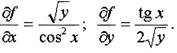
|
Вычислим эти производные при
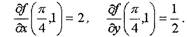
|
Подставим полученные значения в формулу приближенных вычислений:
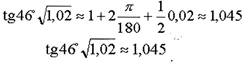 Ответ:
Ответ:
|
Пример.
Найти точки экстремума функции:
Решение.
Найдем критические точки функции. Для этого сначала найдем частные
производные
Решая систему
уравнений
заданная функция экстремума. Находим значения вторых производных в
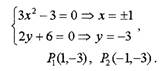
| находим критические точки
|
точке P1:
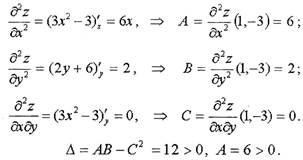
Следовательно, в точке P1 функция z имеет минимум:
Аналогично проводятся исследования для точки
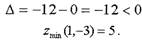
Пример. Вычислить полный дифференциал функции
выполняется равенство F'(x)=f(x) или dF(x)=f(x)dx.
Из дифференциального исчисления известно, что если две функции f(x) и
F' (х) отличаются друг от друга на постоянную величину, то производные или
дифференциалы этих функций равны, т.е. если
то
Известно также, что, и наоборот, если две функции f(x) и F(x) имеют одну и ту же
производную или один и тот же дифференциал, то они отличаются друг от друга на
постоянную величину, т.е. если
Отсюда непосредственно следует, что если в формуле у = F(x) + С мы будем
придавать постоянной С все возможные значения, то получим все возможные
первообразные функции для функции f(х)
Определение 2: Множество F(x) + С всех первообразных функций для данной
функции f(х) , где С принимает все возможные числовые значения, называется
неопределенным интегралом от функции f (х) и обозначается символом
С - произвольная постоянная - const.
f(x) называется подинтегральной функцией
f(x)dx - называется подинтегральным выражением
символ ∫ - знак неопределенного интеграла.
Неопределенным интегралом называют не только множество всех первообразных,
но и любую функцию этого множества. Неопределенный интеграл представляет
собой любую функцию, дифференциал которой равен подинтегральному
выражению, а производная равна подинтегральной функции. Нахождение
первообразной по данной функции f(x) называется интегрированием и является
действием, обратным дифференцированию.
Основные свойства неопределенного интеграла
Таким образом, по определению,
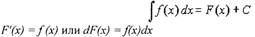
|
| 2. Дифференциал неопределенного интеграла равен подынтегральному
|
1. Производная неопределенного интеграла равна подынтегральной функции:
| 5. Неопределенный интеграл от суммы функции равен сумме интегралов от
|
| 6. Неопределенный интеграл от разности функции равен разности интегралов
|
3. Неопределенный интеграл от производной функции отличается от самой
функции только на постоянную величину:
4. Постоянный множитель можно выносить за знак неопределенного интеграла.
Дата добавления: 2016-06-24; просмотров: 3802;
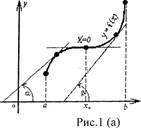
 Рис.1 (б)
Рис.1 (б)
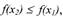
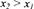
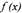
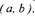

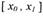
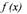
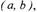
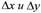
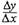
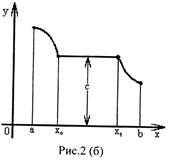
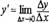
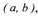
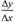
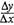
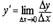
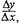

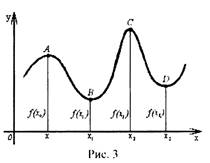
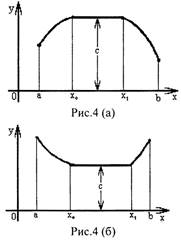
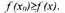
 Рис. 5
Рис. 5
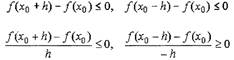
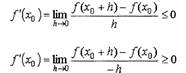
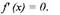
 Рис. 6
Рис. 6
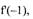
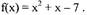
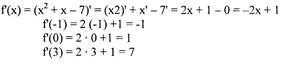
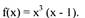
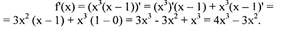
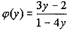
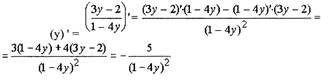
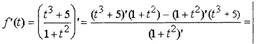
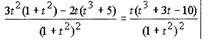
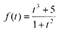
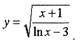
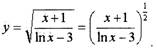
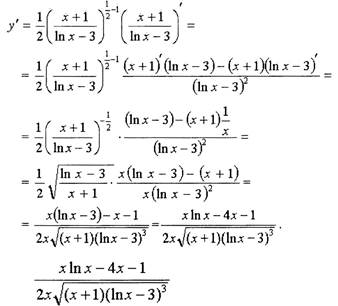 Ответ:
Ответ:
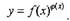 функцию:
функцию:
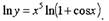
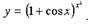
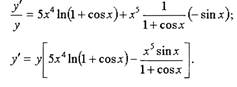
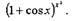
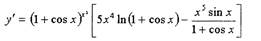
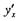
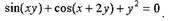
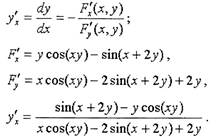
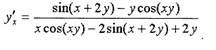
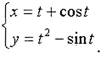
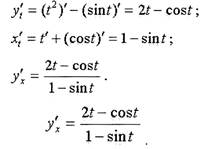 Ответ:
Ответ:
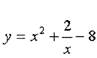
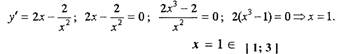
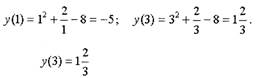 Ответ:
наименьшее значение функции.
Ответ:
наименьшее значение функции.
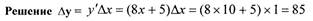
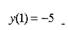
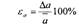
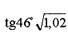
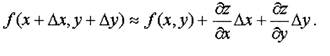
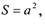
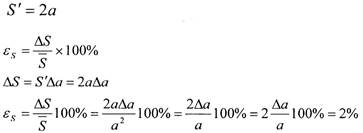 Пример
Пример
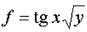
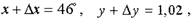
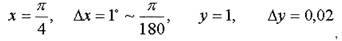
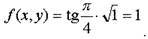
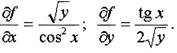
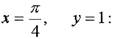
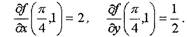
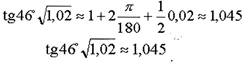 Ответ:
Ответ: