Системы одновременных уравнений.

Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых может, кроме объясняющих переменных, включать в себя также объясняемые переменные из других уравнений системы. Т. о. мы имеем здесь набор объясняемых переменных, связанных через уравнение. Примером, может служить модель спроса и предложения, приведённая ниже. Системы одновременных уравнений требуют относительно более сложный математический аппарат. Они могут использоваться для моделей страновой экономики.

Пусть 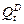- спрос на товар в момент времени t;

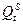- предложение товара в момент t;

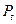- цена на товар в момент времени t;

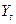- доход в момент времени t;

Составим следующую систему уравнений «спрос-предложение»:

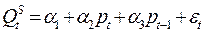(предложение);

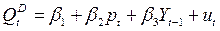(спрос);

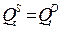(равновесие).

Цена товара 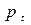и спрос на товар 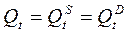определяются из уравнений модели, т. е. являются эндогенными переменными. Предопределёнными переменными в данной модели является доход 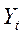и значение цены товара в предыдущий момент времени .

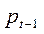Становление и развитие эконометрического метода (ЭМ) происходили на основе «высшей статистики» - на методах парной и множественной регрессии, парной, частной и множественной корреляции, выделении тренда и других компонент временного ряда.

Первый момент. Эконометрика как система специфических методов начала развиваться с осознания своих задач – отражения особенностей экономических переменных и связей между ними.

В уравнение регрессии стали включаться переменные не только I, но и II степени – с целью отразить свойство оптимальности экономических переменных: наличия значений, при которых достигается мини-максное воздействие на зависимую переменную. Так влияние удобрений на урожайность: до определенного уровня насыщение ими почвы способствует росту урожайности, но дальнейшее наращивание после достижения оптимального уровня не приводит к росту урожайности, а может даже вызвать её снижение. То же можно сказать о воздействии многих социально-экономических переменных (возраста рабочего на уровень производительности труда или влияние дохода на потребление продуктов питания и т. д.). В конкретных условиях нелинейность влияния переменных может не подтвердиться, если данные варьируют в узких пределах, т. е. являются однородными.

Второй момент –это взаимодействие социально-экономических переменных, которое может рассматриваться как самостоятельная компонента в уравнении регрессии .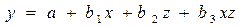

Эффект взаимодействия ( 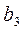) может оказаться статистически незначимым. Поэтому понятие о нелинейности и неаддитивности связей не исключают внимания к проблеме применимости линейных и аддитивных уравнений регрессии.

По Гольдбергеру:

1. Функция 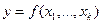линейна по всем независимым переменным тогда и только тогда, когда 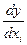не включает 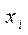, т. е. 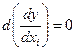, эффект данного изменения по 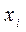не зависит от .

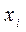2. Функция 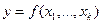является аддитивной по 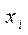, тогда, когда 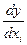не включает 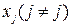, т. к. когда 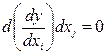- это эффект данного изменения по каждой независимой переменной не зависит от уровня другой переменой.

Например:

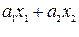
1) 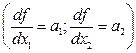- линейна и аддитивна по 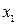и по ;

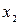2) 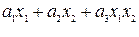- линейна 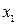по и по 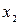, но не аддитивна ;

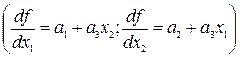3) 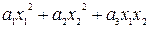- нелинейна 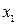по и по 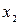, и неаддитивна.

В 30-е годы 20 в. повсеместное увлечение регрессией сменилось разочарованием. Строя уравнение множественной регрессии, и стремясь включить как можно больше переменных, исследователи сталкивались с бессмысленными результатами – с несоответствием знаков при коэффициентах регрессии априорным предположением, а также необъяснимым изменением их значений.

Причина заключается в том, что изолированно взятое уравнение регрессии есть не что иное, как модель «чёрного ящика», поскольку в ней не раскрыт механизм зависимости выходной переменной y от входных переменныхx_i,а лишь констатируется факт наличия такой зависимости.

Для проведения правильного анализа нужно знать всю совокупность связей между переменными. Это позволяет сделать конфликтный анализ (1934 г. Р. Фриш). Он предложил изучать всю иерархию регрессий между всеми сочетаниями переменных. При этом каждая переменная рассматривалась как зависимая от всех возможных подмножеств переменных. Р. Фриш обнаружил «эффект деградации» коэффициентов регрессии. Он проявлялся в том, что если в регрессию включается много переменных, имеющие линейные связи друг с другом (мультиколлинеарные переменные), то коэффициенты регрессии имеют тенденцию возвращаться к тем значениям, которые они имели в уравнении с меньшим числом переменных. Например, при 4х переменных, вводя разное их число в анализ, Фриш получил следующие коэффициенты регрессии для связи между x₁ и x₂:

b₁₂=-0,120; b_12,4=0,919; b_12,3=-0,112.Это позволило ему сделать вывод о наличие какого-то оптимального круга переменных, выход за который не улучшает коэффициенты регрессии, делает их неустойчивыми.

На основе изменения коэффициентов регрессии b_iи множественного коэффициента детерминации R², он разделил все переменные на полезные, лишние и вредные. Переменная считалась полезной, если её включение значительно повышало R², когда этого не происходило, и ввод новой переменной не изменял коэффициентов регрессии при других переменных, она считалась лишней, если добавляемая переменная сильно изменяла b_iбез заметного изменения R² – вредная. Конфликтный анализ, надо отметить не получил большого распространения.

Методы корреляции и регрессии создавались как методы описания совместных изменений 2 и более переменных. Совместные изменения переменных могут не означать наличие связей между ними. Потребность в причинном объяснении корреляции привела американского генетика С. Райта (1910 – 1920) к созданию метода путевого анализа как одного из разновидностей структурного моделирования. Путевой анализ основан на изучении всей структуры причинных связей между переменными, т. е. на построении графа связей и изоморфной ему рекурсивной системы уравнений, которые интерпретируются как путевые коэффициенты (коэффициенты влияния) рассчитываются на основе коэффициентов парной корреляции. Это позволяет проанализировать структуру корреляционной связи с точки зрения причинности. Каждый коэффициент парной корреляции рассматривается как мера полной связи двух переменных.

Путевой анализ позволяет разложить величину этого коэффициента на 4 компоненты:

1. Прямое влияние одной переменной на другую (нет промежуточных звеньев).

2. Косвенное влияние, т. е. передача воздействия одной переменной на другую через промежуточное звено.

3. Непричинная компонента, объясняемая наличием общих причин, воздействующих на одну и другую переменные.

4. Непричинная компонента, зависимая от неанализируемой в модели корреляции входных переменных. Если компоненты прямого и косвенного причинного влияния равны 0, корреляция между ними является ложной (Пирсон К. 1857-1936).

При работе с временными рядами разных показателей и при изучении взаимосвязи между ними довольно быстро были осознаны проблема ложной корреляции и проблема лага, т. е. сдвига во времени, который позволил уловить наличие связей между показателями (ВВП и инвестициями, приёмом на учёбу и выпуском и т. п.)

Ложная корреляция возникла под влиянием фактора времени, т. е. трендовой компоненты в коррелируемых временных рядах, в случаях, если: y_t – уровень одного временного ряда во время t; x_t - уровень другого временного ряда во время t. Связь между ними выражается графом связей:

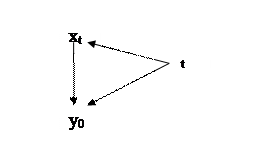
Это привело к идеи измерения корреляции не самих уровней x_t и y_t, первых разностей: 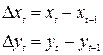при линейных трендах.

Т. О. подводя итоги, отметим, что эконометрический метод складывался в преодолении следующих неприятностей, искажающих результаты применения классических методов:

-ассиметричность связей;

-мультиколлинеарность объясняющих переменных;

-закрытости механизма связи между переменными в изолированной регрессии;

-автокорреляции;

-ложной корреляции;

-наличии лагов.

Эконометрическое исследование включает решение следующей задачи:

· качественный анализ связей экономических переменных - выделение зависимых (y) и независимых (x) ;

· подбор данных;

· спецификация формы и связи между y и x_к;

· оценка параметров модели;

· проверка ряда гипотез о свойствах распределения вероятностей для случайной компоненты (гипотезы о средней, дисперсии и ковариации);

· анализ мультиколлинеарности объясняющих переменных, оценка статистической значимости, выявление переменных, отвечающих за мультиколлинеарность;

· введение фиктивных переменных;

· выявление автокорреляции и лагов;

· выявление тренда, циклической и случайной компонент;

· проверка остатков на гетероскедастичность;

· анализ структуры связей и построение системы одновременных уравнений;

· проверка условий идентификации;

· оценивание параметров системы одновременных уравнений (двухшаговый и трехшаговый МНК, метод максимального правдоподобия);

· моделирование на основе системы временных рядов: проблемы стационарности и коинтеграции;

· построение рекурсивных моделей ARIMA и VAR-моделей;

· проблемы идентификации и оценивания параметров.

Если это укрупнить, то в качестве этапов эконометрического исследования можно указать:

- постановку проблемы;

- получение данных, анализ их качества;

- спецификацию модели;

- оценку параметров;

- интерпретацию результатов.

Этот список проще, чем предыдущий.