Чем собственно занимается

Эконометрист?

Давайте представим себе океанский лайнер водоизмещением 58000т. Корабль построен 30 лет назад, на нём есть залы отдыха, рестораны, бары, кинотеатр, конференц-зал, библиотека, ночной клуб, художественная галерея и торговый центр.

Вопрос: Сколько лет капитану?

Мы не в состоянии ответить на этот вопрос, поскольку доступная нам информация не содержит никакого упоминания о возрасте капитана. Это не совсем так. Лайнер водоизмещением 58000. – очень большой корабль. На его капитане лежит огромная ответственность. И только человек с большим опытом в состоянии справиться с этой работой. В то же время капитан должен обладать хорошей физической формой и быть способным справляться со стрессовыми ситуациями. Здравый смысл подсказывает, что возраст капитана между 40 и 60 годами. Эконометрист, который хочет выглядеть наукообразно, сказал бы, что его оценка возраста капитана равна 50 со стандартным отклонением 5.

Это хороший пример эконометриста за работой. Он показывает, что доступная нам информация обычно недостаточна для решения задачи, и требуются также здравый смысл и знание жизни, а решение 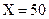, 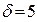(отклонение) сформулировано в вероятностных терминах без достаточных на то статистических оснований.

Реальные примеры из экономики всегда труднее. Большинство эконометристов полагают, что главная цель прикладной эконометрики - сопоставление экономических теорий с наблюдаемыми явлениями. Это включает в себя проверку гипотез, например, теории монетаризма или рационального поведения потребителя. Задача эконометриста (в идеале) было бы проверить, верна ли данная экономическая теория или нет, основываясь на экономических данных и статистическом аппарате. Никто не скажет, что это легко.

Индивидуумы, семьи, фирмы ведут себя так иррационально и их групповое поведение настолько мало предсказуемо, что трудно предположить существование какого-либо закона, претендующего на универсальность. Это сильное утверждение, но оно верно.

Давайте обсудим последствия одного универсального закона. Это знаменитый пример, взятый из жизни, показывает, как один верный закон может быть использован для открытия другого.

Наблюдая спутники Юпитера, астрономы заметили, что иногда они на 8 минут впереди, а иногда на 8 минут отстают от времени, рассчитанного по законам Ньютона. Причем замечено, что спутники опережают расчетное время, когда Юпитер ближе к Земле, и отстают, когда Юпитер удалён. Если мы доверяем теории Ньютона, то должны заключить отсюда, что свет имеет конечную скорость, и то положение спутников, которое мы наблюдаем, является вовсе не их текущим положением, а тем, в котором они находились некоторое время назад, необходимое, чтобы свет дошел от Юпитера до Земли. Олаф Ремер таким образом в 1675 году показал, что свет имеет конечную скорость, и годом позже привёл оценку скорости света 214 000 км/с (ошибся на 30%).

Ничего подобного этой строгой красоте невозможно в эконометрике. Люди, фирмы, организации, их взаимодействие на различных уровнях агрегирования настолько богаче и интереснее планет, что неизбежно являются гораздо более сложными объектами для моделирования и прогноза.

Данные в эконометрике никогда не являются экспериментальными. Не правда, было бы хорошо удвоить цены на сахар, оставив все остальные неизменными и посмотреть на реакцию покупателя. Вероятно, это и было возможно в Советском Союзе, но определенно невозможно в современной России, и, следовательно, эконометрист не может ставить подобные эксперименты.

Все параметры изменяются одновременно. Данные, с которыми должны работать, не являются результатом контролируемого эксперимента. Они не экспериментальные.

В физике, химии, биологии и т. д. можно проводить контролируемые эксперименты, но только не в эконометрике. (Астрономические данные тоже не являются экспериментальными. Мы не можем, например, изменить орбиту Марса, чтобы посмотреть, как это повлияет на орбиту Земли.)

Отсюда новые трудности. Традиционные методы математической статистики – теория оценивания и проверки гипотез были развиты для экспериментальных наук, но не для эконометрики. Поэтому эти методы, не могут быть без какой-либо модификации применены в эконометрике. В математической статистике проверка гипотезы и оценивание её не являются двумя разными темами. Прикладной статистик либо проверяет гипотезу, либо оценивает некоторые параметры, но никогда не делает то и другое одновременно. Эконометрист напротив, должен всё делать одновременно. Поэтому необходима новая теория статистического вывода, которая позволяла бы это делать, но такой теории до сих пор нет.

Теория и практика. Разрыв между ними в эконометрике больше, чем в других науках.

Известная история среди эконометристов иллюстрирует этот разрыв.

Ночь. Некто А идет по улице и видит другого человека Б, что-то ищущего под уличным фонарём. Что вы ищите? – спросил А. «Я потерял ключи», - ответил Б. «Где вы их потеряли?» - снова спросил А. «Там», - ответил Б, указывая на 30 метров в сторону.

«Тогда почему же вы их ищете здесь?» - спрашивает А, являясь человеком практического склада ума. «Там слишком темно», - отвечает Б и продолжает свои поиски под уличным фонарём.

Эконометрический подход к изучению и анализу социально-экономических объектов (явлений, процессов, систем) предполагает построение модели изучаемого объекта. Это является ключевым момен­том при использовании эконометрического подхода. В эконометрике модель относится к классу математических моделей.

Под математической моделью понимают приближенное описание объ­екта (процесса, явления, системы) на языке математики.

Язык математики (математический аппарат, инструментарий) вклю­чает такие средства описания, как таблицы, графики, алгебраические и логические соотношения, неравенства, дифференциальные или разно­стные уравнения, теоретико-множественное описание и т. п. и т. д.

Необходимость построения и использования математических моде­лей обусловлена следующими важными обстоятельствами.

1. Процесс построения математической модели позволяет система­тизировать сложные, взаимосвязанные факторы, выделить существенные и не существенные для изучаемого процесса связи и параметры.

2. Математическое описание позволяет каждому фактору поставить в соответствие математический символ (переменную) и устано­вить взаимосвязь и взаимовлияние одних переменных на другие.

3. Математическая модель, в отличие от вербальной (словесной), дает возможность описать процесс компактно, в виде набора ма­тематических соотношений, абстрагируясь при этом от несуще­ственных деталей, и установить строгие правила поведения пере­менных, характеризующих процесс.

4. При построении математической модели упорядочивается ин­формация, определяется ее ценность и необходимый объем.

5. Математическая модель закладывает основу для количественного анализа поведения объекта путем проведения численного (имита­ционного) эксперимента, что позволяет выявить возможные аль­тернативные сценарии поведения объекта и количественно оце­нить последствия, к которым приведет их реализация. Это особен­но важно при изучении систем, для которых невозможен натурный эксперимент. К таким системам относятся и социально-экономи­ческие системы и процессы. При этом во много раз увеличивается число сценариев, которые удается проанализировать.

6. Математическая модель дает возможность качественно исследо­вать поведение изучаемого объекта. Другими словами, построив математическую модель, се можно изучать в соответствии с пра­вилами математики, абстрагируясь от реального объекта. Это часто позволяет получить новые, нетривиальные знания о самом моделируемом объекте.

7. Математическое моделирование позволяет выявить и оценить влияние скрытых (латентных) факторов.

8. Построение математической модели является основой для эф­фективного применения современных информационных техно­логий. Потребность в их применении обусловлена сложностью используемых математических моделей, необходимостью сбора и обработки больших массивов данных, сложностью вычисли­тельных процедур.

Процесс построения математической модели включает несколько основных этапов, которые перечисляются ниже.

1. Определение цели исследования, качественный анализ и изуче­ние экономического объекта (предметной области), установле­ние общих закономерностей его функционирования, формулировка правдоподобных гипотез и предположений (упрощающих допущений) относительно характера взаимодействия различных элементов объекта и т. д.

2. Анализ и оценка качества имеющихся эмпирических данных. Изучение возможностей получения дополнительной информа­ции и, если необходимо, ее сбор.

3. Построение математической модели с привлечением математи­ческого аппарата, позволяющего адекватно описать поведение объекта.

4. Оценка параметров модели (идентификация) на основе имею­щихся статистических данных. Проверка адекватности модели (ее соответствия данным).

5. Формальный анализ математической модели, исследование ее свойств с целью изучения поведения объекта на качественном уровне.

6. Проведение численных расчетов (экспериментов) и получение количественных результатов.

7. Анализ полученных результатов и их содержательная (экономи­ческая) интерпретация. Выработка рекомендаций для принятия решений.

Современная математика предоставляет богатый арсенал средств для построения математических моделей в естественных науках, технике, экономике и других гуманитарных науках, подкрепленный возможно­стями современных автоматизированных информационных технологий.

1.2 Области применения эконометрических моделей. Методологические вопросы построения эконометрических моделей: обзор используемых методов.

Экономико-математическая модель становится эконометрической, и при се построении и оценке используются эконометрические методы, если ставятся задачи:

а) получения с помощью этой модели количественных результатов на основе статистических данных;

б) ко­личественной проверки гипотез, выдвигаемых экономической теори­ей.

Эконометрические модели применяются для изучения социаль­но-экономических процессов и на макро- и на микроуровнях. Ис­пользование эконометрических методов является необходимым этапом создания количественной модели экономического объекта, независимо от того, для каких целей или в рамках какой дисципли­ны — исследования операций или, скажем, финансовой математики, модель строится (в результате, возникло даже такое понятие, как фи­нансовая эконометрика).

В эконометрике рассматриваются в основном параметрические мо­дели, т. е. структура модели (функциональные зависимости между эко­номическими переменными) задается с точностью до параметров. Оп­ределение вида функциональных зависимостей называется специфика­цией модели. Спецификация модели является ключевым этапом построения любой эконометрической модели.

Здесь возникает проблема выбора структуры модели (специфика­ции). В зависимости от уровня знаний об объекте условно можно выде­лить два наиболее общих класса моделей:

1) поведенческие (behavioural models);

2) феноменологические (phenomenological models).

Поведенческие модели строятся только на основе наблюдений за по­ведением объекта (данных «вход-выход») и приближенно описывают (аппроксимируют) наблюдаемое поведение без какой-либо априорной информации о внутренней структуре объекта (внутренних взаимосвя­зях между переменными). Структура и количество параметров устанав­ливаются в процессе построения модели. Параметры таких моделей могут не иметь какого-либо экономического смысла.

Одна из основных задач эконометрики — разработка методов построе­ния поведенческих моделей.

Феноменологические модели (модели, основанные на знаниях) — это записанные в виде математических соотношений экономические зако­ны, выпеченные па основе экономической теории. Такие модели могут включать уравнения (дифференциальные или разностные), описываю­щие динамику процесса, статические балансовые соотношения (усло­вия равновесия) и т. п., которые следуют из положений экономической теории. Как правило, структура уравнений подобных моделей соответ­ствует гипотезам экономической теории, а количество параметров за­ранее определено и ясен их экономический смысл.

Задача эконометрики при построении феноменологических моделей — подгонка модели (ее параметров) к установленному набору реальных данных, которые получены в результате наблюдения за изучаемым объектом.

Таким образом, построение эконометрической модели позволяет оценить степень достоверности гипотез, выдвигаемых экономической теорией, проверить их на практике. Это, в свою очередь, помогает вы­работать и обосновать рекомендации для проведения экономической политики, спрогнозировать последствия принятия тех или иных эко­номических решений.

В настоящее время Эконометрика располагает огромным разнообразием типов моделей – от больших макроэкономических моделей, включающих несколько сот уравнений, а иногда и тысяч, до малых коинтеграционных моделей, предназначенных для решения специфических проблем.

Модели основываются на экономической теории или на эмпирических данных. Модели должны быть «настолько простыми, насколько это возможно, но не проще» отмечал А. Эйнштейн. В большинстве случаев экономические законы выражаются в относительно простой математической форме. Рассмотрим, например, функцию потребления:

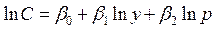; (1)

где 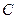- потребление некоторого пищевого продукта на душу населения в некотором году,

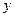- реальный доход на душу населения в этом же году, а

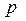- индекс цен на этот продукт, скорректированный (дефлированный) на общий индекс стоимости жизн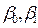и;

и 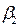- константы.

Это уравнение описывает (в среднем) поведение потребителя по отношению к покупке данного пищевого продукта в зависимости от относительного уровня цен на продукты и реального душевого дохода.

Закон поведения будет определён, как только мы найдём значения коэффициентов 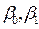и 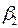. Соответственно задача эконометрики – определить (оценить) эти коэффициенты из подходящего набора наблюдений. Но не единственная задача. Можно задать много других вопросов, также относящихся к эконометрике:

1) нет ли переменных, которые следовало дополнительно включить в уравнение (например, цены на непродовольственные товары);

2) не следует ли исключить из уравнения некоторые переменные;

3) насколько корректно изменены наши данные?

4) верно ли, что модель линейна? Верна ли эта экономическая теория?

5) является ли модель полной? (т. е. учитываем спрос и не рассматриваем предложение);

6) достаточно ли изучать макроэкономическое уравнение или необходимо изучать индивидуальные (микро) данные?

Приведённая выше модель является статистической. Возможно, более подходящей была динамическая модель. Т. е. можно предположить, что прошлогодний доход может влиять на текущий уровень потребления. Т. о. его также необходимо включить в уравнение.

Эконометрика рассматривает все эти вопросы.