Понятие о функциональной, статистической и корреляционных связях. Основные задачи корреляционно-регрессионного анализа.

Различают 2 основных формы причинных зависимостей:

Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует определённое значение другой. Такой зависимостью связаны, например, радиус круга и его площадь, количество купленного товара и его стоимость, количество потребляемой абонентом электроэнергии и плата за неё и другое.

Однако часто встречаются переменные величины, которые являются зависимыми, но каждому значению одной соответствует не определённое, а некоторое множество значений другой, причём число значений и сами эти значения не отражают определённой закономерности.

Множество значений переменной y, соответствующих фиксированному значению переменной x, будем рассматривать как соответствующее ему распределение переменной y.

Переменные величины x и y связаны статистически, если каждому значению одной из них соответствует распределение другой, меняющееся с изменением первой величины и по вариантам и по частотам.

Таким образом, при корреляционной связи каждому значению аргумента соответствует не одно, а несколько значений функции и между ними нет тесной зависимости. Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и групповыми средними другой.

(y на x) 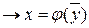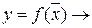(x на y)

Уравнения, выражающие в общем виде корреляционные зависимости, называются корреляционными уравнениями или уравнениями регрессии.

Различают линейные и нелинейные регрессии.

Линейная регрессия: 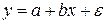или .

Нелинейные регрессии делятся на два класса:

1) регрессии, нелинейные относительно включённых в анализ объясняющих переменных, но линейные по оцениваемым параметрам:

· полиномы разных степеней: ;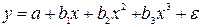

· равносторонняя гипербола: ;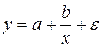

2) регрессии, нелинейные по оцениваемым параметрам:

· степенная: ;

· показательная: ;

· экспоненциальная: .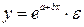

В зависимости от количества факторов, включённых в уравнение регрессии, принято различать: простую (парную) и множественную регрессии.

Простая регрессия – представляет собой регрессию между двумя переменными y и x, то есть вида , где 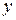- зависимая переменная (результативный признак); 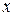- независимая или объясняющая переменная (признак – фактор).

Множественная регрессия – представляет собой регрессию результативного признака с двумя и большим числом факторов, то есть модель вида .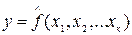

Любое эконометрическое исследование начинается о спецификации модели, то есть с формулировки вида модели, исходя из соответствующей теории связи между переменными. То есть исследование начинается с теории, устанавливающей связь между явлениями.

Прежде всего, из всего круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.

Рассмотрим гипотезу: величина спроса y на товар А находится в обратной зависимости от цены x

в уравнении регрессии корреляционная связь признаков представлена в виде функциональной связи, выраженной соответствующей математической функцией.

Статистические связи между переменными изучаются методами корреляционного и регрессионного анализа.

Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными.

Основной задачей корреляционного анализа – выявление связей между случайными переменными и оценка её тесноты.

Этапы эконометрического моделирования:

1. Постановочный этап, на котором опре­деляются конечные цели и задачи исследования, а также число включенных в модель факторных и результативных экономических переменных.

Цели эконометрического исследования:

1) анализ изучаемого экономического процес­са (явления, объекта);

2) прогноз экономических показателей, харак­теризующих изучаемый процесс (явление, объект);

3) моделирование поведения процесса при раз­личных значениях факторных переменных;

4) формирование управленческих решений.

Количество переменных, включенных в эконометрическую модель, не должно быть слишком большим и должно быть теоретически обоснован­ным. В модели должна отсутствовать функцио­нальная или тесная корреляционная связь между факторными переменными, что может привести к явлению мультиколлинеарности.

2. Априорный этап, на котором осуществ­ляется теоретический анализ сущности изучаемого процесса, а также формализуется априор­ная информация.

3. Этап параметризации, на котором проис­ходит выбор общего вида модели, а также опреде­ляется состав и формы формирующих ее связей.

Задачи, решаемые на этапе параметризации:

1) задача выбора наиболее подходящего вида функциональной зависимости результативной переменной от факторных переменных.

При возникновении ситуации выбора между линейной и нелинейной формами зависимости предпочтение всегда отдается линейной форме как более простой;

2) задача спецификации модели:

а) аппроксимация математической формой обнаруженных связей и соотношений меж­ду параметрами модели;

б) определение зависимых и независимых переменных;

в) выражение исходных предпосылок и огра­ничений модели.

4. Информационный этап, на котором со­бирается требуемая статистическая информация и осуществляется анализ качества собран­ных данных.

5. Этап идентификации модели, на кото­ром реализуется статистический анализ мо­дели и происходит оценивание ее параметров.

6. Этап оценки качества модели, на ко­тором проверяются достоверность и адекватность модели. Созданная модель должна быть адекватна реальному экономическому процес­су. При неудовлетворительном качестве моде­ли возвращаются ко второму этапу моделиро­вания.

7. Этап интерпретации результатов мо­делирования.

В эконометрике применяется два основных типа выборочных данных:

1) пространственные;

2) временные.

Пространственные данные — это совокуп­ность экономической информации, характери­зующей разные объекты и полученной за определенный период или момент времени.

Пространственные данные являются выбороч­ной совокупностью из некоторой генеральной совокупности (например, совокупность различной информации по какому-либо предприятию—размер основных фондов, численность работников).

Временные данные — это совокупность экономической информации, характеризующей определенный объект, но за различные периоды времени. Отдельный временной ряд можно считать выборкой из бесконечного ряда значений показателей во времени (например, данные о динамике фондовых индексов).

Существуют определенные отличия временного ряда или ряда динамики от пространственной выборки:

1) элементы ряда динамики естественным образом упорядочены во времени в отличие от пространственных данных;

2) элементы ряда динамики не являются статистически независимыми в отличие от элементов случайной пространственной выборки, т.е. они подвержены зависимости между прошлыми и настоящими наблюдениями временного ряда (автокорреляции);

3) элементы ряда динамики не являются оди­наково распределенными величинами.

Набор переменных — это совокупность экономической информации, характеризующей

изучаемый процесс или объект. В эконометрической модели используются:

1) результативные (зависимые) перемен­ные, которые в эконометрике называются объясняемыми переменными;

2) факторные (независимые) перемен­ные, которые в эконометрике называются объясняющими переменными.

Среди экономических переменных, вклю­ченных в эконометрическую модель, выделяют:

1) экзогенные (независимые) перемен­ные (х), значения которых задаются извне. В определенной степени данные переменные являются управляемыми;

2) эндогенные (зависимые или взаимоза­висимые) переменные (у), значения кото­рых определяются внутри модели;

3) лаговые (экзогенные или эндогенные) переменные, которые относятся к предыду­щим моментам времени и находятся в урав­нении с переменными, относящимися к текуще­му моменту времени. Например, х_t-1 — лаговая экзогенная переменная, у_t-1 — лаговая эндо­генная переменная;

4) предопределенные (объясняющие) пе­ременные, к которым относятся лаговые (х_t-1), текущие (х) экзогенные переменные и лаго­вые эндогенные переменные (у_t-1).

Основная цель эконометрического модели­рования — это характеристика значений одной или нескольких текущих эндогенных переменных в зависимости от значений предопределенных (объясняющих) переменных.

Примеры типичных практических задач, для решения которых можно применять методы регрессионного анализа:

Пример 1. Исходя из житейского опыта, и опираясь на анализ дан­ных, публикуемых риэлтерскими фирмами, можно предположить, что рыночная цена квартиры (объясняемая, эндогенная переменная) зави­сит от ее характеристик (объясняющих, экзогенных переменных). В их числе: количество комнат; общая и жилая площадь; площадь кухни; этаж; наличие проходных комнат; район города; кирпичный дом или панельный; средний уровень доходов населения данного региона; воз­раст квартиры; наличие балкона или лоджии; стоимость ремонта.

Применение эконометрических методов позволяет установить ко­личественную взаимосвязь между ценой и характеристиками квартиры и ответить на вопрос о том, как преобразуется цена при изменении ха­рактеристик.

Пример 2. Цена товара в некоторый период (эндогенная перемен­ная) зависит от объемов его поставок в этот период, цен конкурирую­щих товаров и, возможно, от времени года (сезона) (экзогенные пере­менные). С помощью регрессионной модели удастся оценить, как из­менится цена товара при колебании объемов поставок или цен конкурентов в зависимости от времени года.

Пример 3. Спрос на некоторый товар (эндогенная переменная) зави­сит от его цены, цен аналогичных товаров, производимых конкурента­ми, от реальных доходов потребителей в данном регионе (экзогенные переменные). Как изменится спрос при изменении экзогенных пере­менных?

Пример 4. Объем сбыта продукции зависит от затрат на рекламу. Мо­дель позволяет оценить эту зависимость количественно и спрогнозиро­вать сбыт при колебании затрат на рекламу в пределах конкретной сум­мы, а также определить рациональный объем этих расходов.

Пример 5. Регрессионный анализ дает возможность установить функциональную зависимость эффективности работы предприятия (например, такого показателя, как рентабельность) от таких факторов, как удельный вес предприятия на рынке, расходы на маркетинг, науч­ные исследования, качество товаров, объем инвестиций, зарплата ме­неджеров.

Пример 6. Как доходность акций некоторой корпорации зависит от доходности рыночного индекса (скажем, индекса РТС)?

Пример 7. Доходность финансовых активов зависит от темпов при­роста валового продукта, уровня процентных ставок, степени инфляции, уровня цен на нефть. Как изменится доходность конкретной цен­ной бумаги при трансформации цен на нефть?

Пример 8. Оклад менеджера зависит от количества персонала в его подчинении, уровня квалификации и окладов менеджеров конкури­рующих предприятий аналогичного профиля. Регрессионная модель позволяет ответить на вопрос о том, каким должен быть справедливый размер оклада руководителя вновь открывающегося филиала.

Пример 9. Торговая фирма имеет множество филиалов. Руководство компании хотело бы количественно оценить, как ежеквартальный то­варооборот филиалов зависит от величины торговой площади и средне­дневной интенсивности потока покупателей и на основе этого принять решение об открытии нового филиала. Обоснованное решение можно принять, прибегнув к методам регрессионного анализа.

Данные, характеризующие различные объекты (например, квартиры) и относящиеся к одному моменту или периоду времени, называются про­странственными.

Отметим, что экзогенные переменные (например, характеристики конкретной квартиры, см. пример I) могут быть как количественными (жилая площадь), так и качественными (панельный или кирпичный дом). Ясно, что никакая, даже очень подробная модель, не в состоянии учесть все факторы, влияющие на пену квартиры, поэтому цена каждой конкретной квартиры зависит от экзогенных переменных неоднознач­но, содержит случайную составляющую.