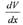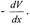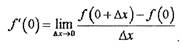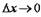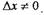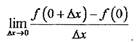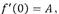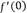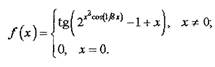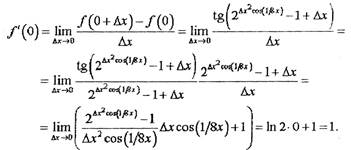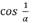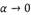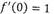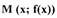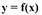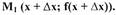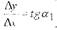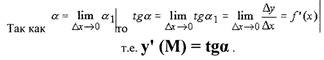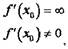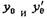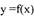1 страница. Определение 1. Производной функции f(x) в точке х называется
ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ. ТАБЛИЦА ПРОИЗВОДНЫХ
Определение 1. Производной функции f(x) в точке х называется
Производная - это предел отношения приращения функции к приращению
ее аргумента при стремлении приращения аргумента к нулю, характеризует
скорость изменения функции. Функция, имеющая конечную производную,
называется дифференцируемой функцией.
Процесс вычисления производной называется дифференцированием.
Из определения следуют основные правила дифференцирования:
1. (const)' = с' = 0.
Производная любого постоянного числа равна нулю.
Примеры:
• (5)' = 0;
• (-8)' = 0;
• (232)'= 0.
2. (х)' = 1.
Производная аргумента равна 1.
3. (с u)' = с u'.
Постоянное число можно выносить за знак производной.
Пример:
• (5 х)' = 5 х' = 5 • 1=5.
4. (u + v - w + ... + s)' = u' + v' - w' + ... + s'.
Производная алгебраической суммы любого числа слагаемых равна этой же
алгебраической сумме производных слагаемых.
Примеры:
• (Зх - 8)' = (Зх)' - (8)' = 3• 1-0 = 3;
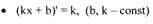 5. Если
5. Если
|
Если u = х, то (хn)' = n хn-1.
Примеры:
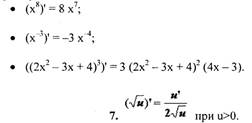
|
Примеры:
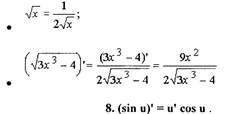
|
Производная синуса сложной функции равна произведению производной этой сложной функции на косинус этой функции. Если u = х, то (sin х)' = cos х . Примеры:
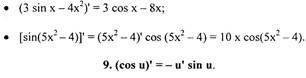
|
Производная степени функции un равна произведению показателя
степени на функцию, в степени на единицу меньше, на производную
самой функции.
Производная косинуса сложной функции равна минус произведению
производной этой сложной функции на синус этой функции.
Если u = х, то (cos х)' = - sin х.
Примеры:
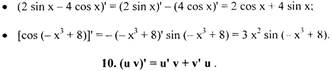
|
Производная произведения равна сумме произведений производной первого сомножителя на второй и производной второго сомножителя на первый. Примеры:
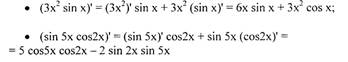
|
Пример 1. Найти производную функции у = Зх + 5: Решение:
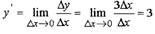
|
Пример 2. Доказать, используя лишь определение, что
| что требовалось доказать.
|
Вынося в последнем равенстве логарифм за знак предела, мы
воспользовались непрерывностью функции
| гарантирует, что при достаточно малом
|
| что необходимо для существования
|
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
| сложная функция аргумента
|
| дифференцируемые по своим аргументам,
|
| находится по следующей формуле:
|
тогда производная функции
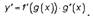
|
Пример а). Найдите производную функции
Воспользуемся формулой
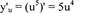
|
Найдем:
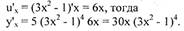
|
| Пример в). Найдите производную функции:
|
| Пример с). Найдите производную функции:
|
ПРИЕМЫ ДИФФЕРЕНЦИРОВАНИЯ
1. Для функций, представляющих собой громоздкие произведения и
частные различных степенных выражений, удобно, а для показательно-
степенных функций, где от переменного зависят как основание
степени, так и ее показатель, - необходимо применять прием
логарифмического дифференцирования.
Этот прием основан на соотношении
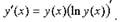
|
где
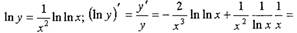
|
Решение:
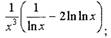
|
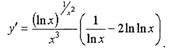 Пример №2. Вычислить
Пример №2. Вычислить
|
Старшие производные функции одной переменной
| Определение производной n -го порядка функции
|
| Определение 2. Производной порядка
|
характер.
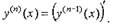 Таким образом,
Таким образом,
|
| производная определяется и вычисляется через
|
| • Пример. Вычислить производную
|
Решение:
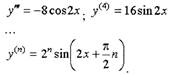
|
Последняя формула является предположением, основанным на предыдущем
утверждении. Для n = 1,2,3,4 она выполняется. Предположим, что
"угаданная" формула для производной (n-1) -го порядка верна. Покажем,
по x:
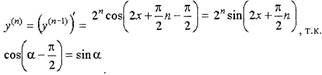 Примененный способ доказательства называется методом полной математической индукции. Впрочем, по индукции можно доказать формулу
Примененный способ доказательства называется методом полной математической индукции. Впрочем, по индукции можно доказать формулу
|
| , а затем, применив ее и формулу
|
• Пример. Посчитаем 2-ю производную из примера № 1,
что тогда она верна и для n-й производной. Пусть
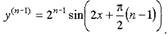
|
| Продифференцируем последнее равенство
|
проиллюстрировав применение логарифмического дифференцирования
для нахождения старших производных.
Продифференцируем
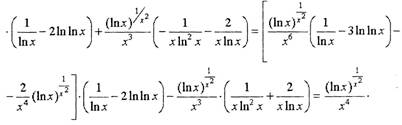
|
При вычислении
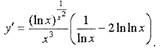
|
использовалась уже найденная в примере № 1
Механический смысл производной
Производная функции у=f(x) в точке x0 выражает скорость
изменения функции в точке x0 , то есть скорость протекания
процесса, описанного зависимостью у=f(x).
V - скорость.
Пусть
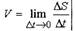
|
| закон прямолинейного движения. Тогда
|
| выражает мгновенную скорость движения в момент времени
|
Первая производная от пути по времени, т.е.
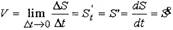
|
а - ускорение
| выражает мгновенное ускорение в момент
|
| (вторая производная от пути по
|
Первая производная от скорости по времени
времени), т.е.ускорение
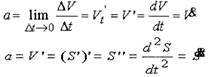
|
| обозначения производных по времени, введенные
|
И.Ньютоном. Он впервые сформулировал, что с позиции механики
мгновенная скорость прямолинейно движущейся точки есть первая
производная от пути по времени, а её мгновенное ускорение есть
первая производная от скорости по времени или вторая производная от
пути по времени.
решение
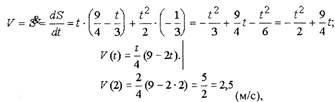 т.е. на 2-й секунде бега спринтер имеет скорость 2,5 м/с.
т.е. на 2-й секунде бега спринтер имеет скорость 2,5 м/с.
|
| • Пример. Найти скорость спринтера через 2 с после старта, если
|
| его путь изменяется по формуле:
|
• Пример . По условию вышеприведенного примера найти
ускорение спринтера в начале бега, т.е. при t0 = 0.
решение
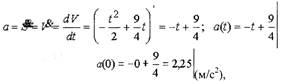 т.е. в начале бега спринтер имел ускорение 2,25 м/с2
т.е. в начале бега спринтер имел ускорение 2,25 м/с2
|
В медицине и биологии, например, используя производную, можно
определить быстроту изменения различных параметров системы или
процесса в живом организме.
• Пример. При воздействии внешней среды давление на
поверхность тела с течением времени меняется по закону
Определите с какой скоростью изменяется давление на 10 секунде от начала
процесса.
решение
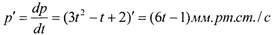 В момент времени t = 10 с
В момент времени t = 10 с
|
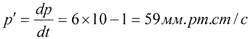 Ответ: В момент времени t = 10 с давление изменяется со скоростью 59 мм.рт.ст. в секунду.
Ответ: В момент времени t = 10 с давление изменяется со скоростью 59 мм.рт.ст. в секунду.
|
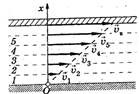
• В качестве примера можно рассмотреть понятие градиента.
На рисунке представлено распределение скоростей разных слоев
жидкости 1-5 при движении вязкой жидкости между двумя
пластинами, из которых нижняя неподвижна, а верхняя движется со
скоростью VB.
Слой у основания неподвижен. По мере приближения к
верхней пластинке скорость слоев возрастает и
стремится к VB. При характеристике возникающих сил
трения между слоями используется важный показатель
dV
—, в данном случае характеризующий изменение
dx
скорости на некотором участке в направлении х,
перпендикулярном скорости, отнесённое к длине этого участка. Величина
называется градиентом скорости или скоростью сдвига. В медицине,
при рассмотрении движения крови по сосудам и анализе вязкости крови,
| оценивают значение скорости сдвига
|
Задача 1: Исходя из определения производной, определите производную
функции f(х) в точке х = 0.
решение
1. По определению производной
Необходимо отметить, что при вычислении предела
2. Вычисляем предел
| 3. Если предел существует и равен А, то
|
Задача 2. Определить по известной функции f(х)
решение
Исходя из определения производной, имеем:
| не определен, этот параметр является
|
конечной величиной. Т.е. заданная функция в точке х = 0 имеет производную
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
| существует касательная к данной
|
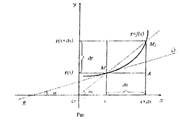
Пусть в точке
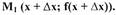
|
| кривой (рис.). Дадим аргументу х приращение Δх и отметим па кривой точку
|
| Проведем секущую ММ1 и обозначим через ɑ1
|
| величину угла, образованного секущей с положительным направлением оси ОХ.
|
| точка M1 будет перемещаться вдоль кривой, приближаясь к точке М, то при этом секущая ММ1 и величина ɑ1 меняются с изменением х. Предельным
|
положением секущей будет прямая, касательная к кривой в точке М,
образующая с положительным направлением оси ОХ некоторый угол,
величину которого обозначим через α.
| 3. Подставляя найденные значения получаем уравнения касательной и
|
Итак, с позиции геометрии производная функции у в заданной ее точке
М есть тангенс угла наклона касательной, проведенной в точке М, с
положительным направлением оси ОХ.
Пользуясь геометрическим смыслом производной, решим следующие
задачи:
Дата добавления: 2016-06-24; просмотров: 8880;
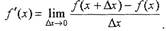
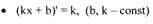 5. Если
5. Если
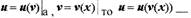
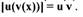
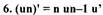
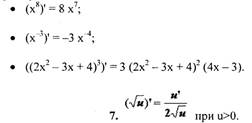
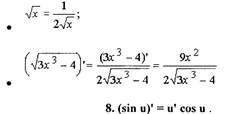
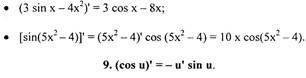
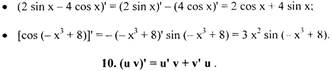
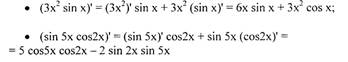


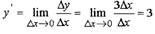
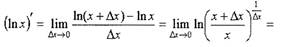
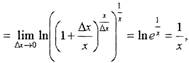
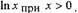
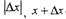
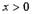
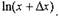
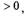
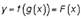
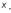
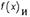
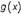
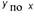
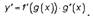
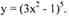
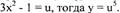
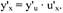
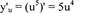
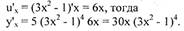
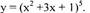
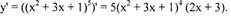
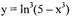
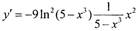
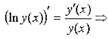
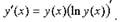
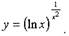
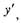
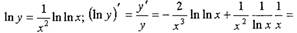
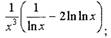
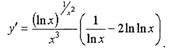 Пример №2. Вычислить
Пример №2. Вычислить
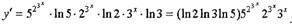
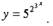
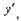
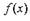
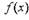
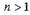
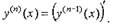 Таким образом,
Таким образом,
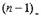
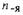
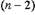
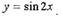
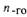
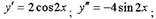
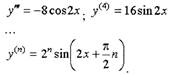
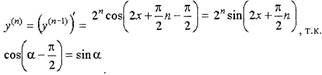 Примененный способ доказательства называется методом полной математической индукции. Впрочем, по индукции можно доказать формулу
Примененный способ доказательства называется методом полной математической индукции. Впрочем, по индукции можно доказать формулу
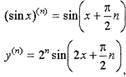
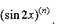
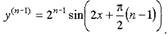
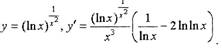
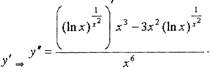
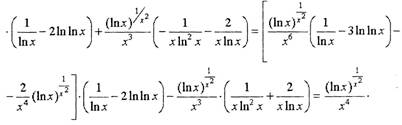
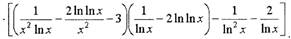
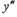
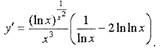
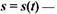
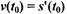
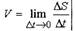
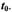
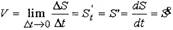
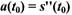
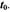
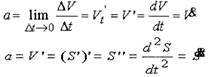
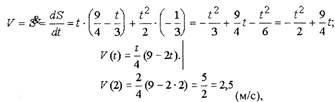 т.е. на 2-й секунде бега спринтер имеет скорость 2,5 м/с.
т.е. на 2-й секунде бега спринтер имеет скорость 2,5 м/с.
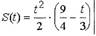
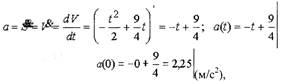 т.е. в начале бега спринтер имел ускорение 2,25 м/с2
т.е. в начале бега спринтер имел ускорение 2,25 м/с2
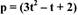
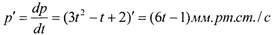 В момент времени t = 10 с
В момент времени t = 10 с
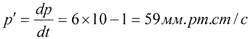 Ответ: В момент времени t = 10 с давление изменяется со скоростью 59 мм.рт.ст. в секунду.
Ответ: В момент времени t = 10 с давление изменяется со скоростью 59 мм.рт.ст. в секунду.