2 страница. Таким образом, с помощью случайной выборки домохозяйств из генеральной совокупности можно точно оценить покупательское поведение всей целевой совокупности
| Семья № | Среднее количество приобретенных баллончиков средства Raid |
| 1, 4, 7, 11, 16 | 2,0 |
| 3, 7, 12, 17, 19 | 2,0 |
| 5, 12, 14, 15, 20 | 2,2 |
Таким образом, с помощью случайной выборки домохозяйств из генеральной совокупности можно точно оценить покупательское поведение всей целевой совокупности. При этом простая случайная выборка отвечает двум характеристикам хорошей выборки: она эффективна и позволяет надежно обобщать результаты на ту генеральную совокупность, из которой была извлечена.
Систематическая случайная выборка. Вариантом простой случайной выборки является систематическая случайная выборка. Систематическая случайная выборка обычно обеспечивает результаты, идентичные получаемым с помощью простой случайной выборки, имея при этом одно дополнительное преимущество — простоту, поскольку отпадает необходимость использовать таблицу случайных чисел.
Так же, как и при простой случайной выборке, систематическая выборка начинается с определения основы, чаще всего в виде перечня, представляющего генеральную совокупность. Имея такой список, можно предпринимать следующие шаги:
· подсчитать количество элементов в списке;
· определить желаемый размер выборки;
· вычислить интервал, через который будут отбираться единицы;
· выбрать в списке случайный пункт;
· отбирать и опрашивать элементы через заданный интервал.
Например, представьте, что имеется список с именами 10 тысяч врачей, из которых, в конечном итоге, требуется отобрать 500. Интервал будет равняться 20 (подсчитывается как 10 000 : 500). Начинать следует со случайного пункта в списке, например с имени врача под номером 16, а затем выбирать имя каждого двадцатого врача, начиная с этого пункта (имя врача под номером 36, 56 и т.д.).
Давайте снова вернемся к генеральной совокупности, показанной в табл. 8.1. Как подтверждает следующая таблица, систематическая выборка позволяет получить точные оценки среднего значения в генеральной совокупности. (Первое число в каждой выборке является начальным пунктом. Интервал равен четырем.)
| Семья № | Среднее количество приобретенных баллончиков средства Raid |
| 1, 5, 9, 13, 17 | 2,0 |
| 2, 6, 10, 14, 18 | 1,8 |
| 11, 15, 19, 3, 7 | 2,2 |
Стратифицированная случайная выборка. В приведенных выше примерах схемы простой и систематической случайной выборки сработали хорошо. Они были эффективны и обеспечили возможность надежно распространить выводы на генеральную совокупность. Однако эти формы выборки сработали хорошо только потому, что генеральная совокупность являлась однородной в отношении измеряемой величины. Иными словами, характер покупок не слишком отличается от семьи к семье. Как показывает нижеприведенная таблица, число приобретенных баллончиков средства Raid существенно не меняется в подгруппах, отличающихся географическим расположением и наличием детей.
| Подгруппа | Среднее количество баллонов приобретенного средства Raid |
| Город | 2,0 |
| Пригород | 2,0 |
| Нет детей | 1,8 |
| Есть дети | 2,2 |
| Город, нет детей | 1,8 |
| Город, есть дети | 2,2 |
| Пригород, нет детей | 1,8 |
| Пригород, есть дети | 2,2 |
Таблица 8.2. Гипотетическая генеральная совокупность для изучения покупательского поведения при приобретении воска для мебели и средств для полировки
| Семья № | Географическая зона | Наличие детей в семье | Количество приобретенных баллонов воска или полировочных средств, шт. |
| 1. | Город | Нет | |
| 2. | Город | Нет | |
| 3. | Город | Нет | |
| 4. | Город | Нет | |
| 5. | Город | Нет | |
| 6. | Город | Есть | |
| 7. | Город | Есть | |
| 8. | Город | Есть | |
| 9. | Город | Есть | |
| 10. | Город | Есть | |
| 11. | Пригород | Нет | |
| 12. | Пригород | Нет | |
| 13. | Пригород | Нет | |
| 14. | Пригород | Нет | |
| 15. | Пригород | Нет | |
| 16. | Пригород | Есть | |
| 17. | Пригород | Есть | |
| 18. | Пригород | Есть | |
| 19. | Пригород | Есть | |
| 20. | Пригород | Есть | |
| Всего в среднем | 3,1 |
Однако ни простая, ни систематическая случайные выборки не дают возможности сделать достоверные обобщения на всю генеральную совокупность, если однородность совокупности уменьшается, а различия между подгруппами внутри совокупности увеличиваются.
Проанализируйте данные, приведенные в табл. 8.2. Целевая совокупность и основа выборки состоят из тех же двадцати семей, что и в примере, иллюстрирующем уровень приобретения средства Raid. А теперь представьте себе, что компания S.E. Johnson намеревается оценить уровень приобретения семьями за последние три месяца воска для мебели и средств для полировки. Как видно из таблицы, приведенной ниже, простые случайные выборки из этой генеральной совокупности дают существенно различающиеся результаты. Вследствие этого можно сделать противоречивые и неточные обобщения покупательского поведения на все население. (Подобный же результат наблюдается и при использовании систематической случайной выборки.)
| Семья № | Среднее количество баллонов приобретенного воска и средства для полировки |
| 1, 5, 9, 13, 17 | 2,6 |
| 10, 11, 17, 19, 20 | 4,0 |
| 3, 12, 14, 16, 19 | 4,4 |
Простая случайная выборка малопригодна в этом случае, так как в генеральной совокупности изучаемый признак варьирует в широких пределах, и эта вариативность обусловлена определенными демографическими или географическими факторами. В данном случае это географическое положение и наличие детей. Частота покупки существенно различается в подгруппах, выделяемых по указанным факторам.
| Подгруппа | Среднее количество баллонов приобретенного воска или средства для полировки |
| Город | 1,5 |
| Пригород | 4,7 |
| Нет детей | 2,5 |
| Есть дети | 3,7 |
| Город, нет детей | 1,0 |
| Город, есть дети | 2,0 |
| Пригород, нет детей | 4,0 |
| Пригород, есть дети | 5,4 |
Пользоваться стратифицированной случайной выборкой следует в том случае, если вы предполагаете, что существует значительная вариативность изучаемой переменной, вызванная или связанная с наблюдаемыми характеристиками единиц в генеральной совокупности, из которой извлекается выборка. Можно допустить, что семьи, в которых нет детей (меньше отпечатков пальцев на мебели), пользуются этим товаром реже, чем семьи, в которых есть дети, и что семьи, проживающие в городе (дома и квартиры поменьше с меньшим количеством мебели), также пользуются этим товаром реже по сравнению с семьями, проживающими в пригороде. Следовательно, можно выделить слои (стратифицировать совокупность), т.е. разделить семьи из целевой генеральной совокупности на четыре класса (или слоя), à потом извлекать случайную выборку отдельно из каждого слоя[7].
Таким образом, реализация стратифицированной выборки — это трехступенчатый процесс.
· Во-первых, устанавливаются критерии классификации слоев (страт). Эти критерии должны задавать непересекающиеся классы единиц отбора. Критериями классификации для генеральной совокупности, указанной в табл. 8.2, являются место проживания и наличие детей. Руководствуясь этими критериями, можно получить четыре отдельных слоя: 1-й — проживающие в городе и не имеющие детей, 2-й — проживающие в городе и имеющие детей, 3-й — проживающие в пригороде и не имеющие детей, 4-й — проживающие в пригороде и имеющие детей.
· Во-вторых, каждый элемент, включенный в основу выборки, назначается одному-единственному слою. Семьи, о которых идет речь в табл. 8.2, будут распределены таким образом: 1-й — семьи 1–5, 2-й — семьи 6–10, 3-й — семьи 11–15 и 4-й — семьи 16–20.
· В-третьих, из каждого слоя независимо извлекается случайная выборка (с применением или простого, или систематического отбора).
Третью ступень — отбор из каждого отдельного слоя — можно проводить одним из двух вариантов в зависимости от количества элементов, выбираемых из каждого отдельного слоя. Можно использовать пропорциональную и непропорциональную выборку.
При пропорциональной стратифицированной выборке единицы отбираются пропорционально доле слоя в целевой совокупности. Например, каждый из четырех слоев генеральной совокупности, продемонстрированной в табл. 8.2, составляет 25% всего населения. В результате при пропорциональном стратифицированном отборе по 25% исследуемой выборки будут извлечены из каждого слоя. Пропорциональная стратифицированная выборка эффективна тогда, когда общее количество слоев невелико и их размеры относительно равнозначны.
Если же абсолютное количество слоев велико и их размеры несопоставимы, при применении пропорциональной стратифицированной выборки могут возникать проблемы. Когда некоторые из слоев невелики, пропорциональная выборка не обеспечит необходимого количества наблюдений или интервью для проведения надежного анализа данных. В этих случаях используют непропорциональную стратифицированную выборку.
Непропорциональная стратифицированная выборка отбирает заданное количество элементов из каждого слоя независимо от относительной величины этих слоев. Отбор обусловливается соображениями последующего анализа, т.е. необходимостью получить выборку такого объема, который бы обеспечил надежный анализ данных, в противоположность соображениям, связанным с генеральной совокупностью (т.е. доле слоя в генеральной совокупности). Если используется непропорциональная стратифицированная выборка, данные, полученные по каждому из слоев, необходимо взвесить для того, чтобы компенсировать разницу между долей слоя в выборке и в генеральной совокупности. Только после подобного взвешивания представляются обобщенные результаты по выборке в целом. Врезка 8.2 иллюстрирует процесс формирования непропорциональной стратифицированной выборки и взвешивание данныхпо каждому слою для определения общих характеристик совокупности.
Врезка 8.2. Непропорциональная выборка
Пиццерия Килито намерена определить восприятие потребителями качествà своего товара. Генеральная совокупность выборки была разделена на три слоя:
· лица, попробовавшие товар и купившие его вновь хотя бы раз (по подсчетам, составляют 65% генеральной совокупности);
· лица, попробовавшие товар, но не купившие его вновь (30% генеральной совокупности);
· лица, никогда не пробовавшие товар (5% генеральной совокупности).
Для анализа интервьюируются по 100 представителей из каждого слоя. В процессе интервью респондентам задается вопрос: “Какую оценку по шкале от 1 до 10, где 10 — самый высокий балл, вы бы дали качеству товаров, изготовляемых в пиццерии Килито?”
Среднее количество баллов по каждому из слоев выглядит таким образом.
| Слой | Количество участников опроса, чел. | % от генеральной совокупности | Оценка качества в среднем, балл |
| Совершившие повторную покупку | 7,7 | ||
| Отказавшиеся от повторной покупки | 2,3 | ||
| Никогда не пробовавшие | 4,7 | ||
| Общий средний балл по совокупности | 5,93 |
Общий средний балл оценки товара, составивший 5,93, подсчитывается таким образом: (7,7 ´ 0,65) + (2,3 ´ 0,30) + (4,7 ´ 0,05).
Ошибки случайной выборки
Цель случайной выборки — отбор группы лиц или объектов, представляющих генеральную совокупность, из которой они были извлечены. Однако исследователи должны внимательно следить, чтобы отбор людей или объектов, попавших в выборку, проводился таким способом, который не приводит к смещениям. Устранение смещений очень важно, поскольку только в их отсутствие исследователь сможет с уверенностью распространять результаты исследования на генеральную совокупность, из которой извлекалась выборка.
Смещение выборки возникает тогда, когда члены интересующей исследователя генеральной совокупности отбираются с нарушением основного принципа случайного отбора, т.е. им не предоставляется известный и равный шанс быть отобранными и включенными в выборку. Использование телефонной книги как источника номеров для телефонного опроса, скорее всего, приведет к смещению выборки. Даже при случайном отборе имен и номеров из телефонной книги смещение будет иметь место, так как лица, не внесенные в книгу, автоматически исключаются из исследований (именно по этой причине метод случайного набора телефонных номеров может оказаться более предпочтительным). Ниже приведены дополнительные примеры возникновения смещения при отборе[8].
Представьте, что вам понадобилось сформировать случайную выборку из числа студентов вашего университета. Вы добросовестно пытаетесь провести беседу с каждым десятым студентом, входящим в кафетерий. Местом проведения интервью вы выбрали кафетерий, потому что большинство студентов бывают там, по крайней мере, один раз в день. Тем не менее, поскольку студенты заходят в кафетерий с различной периодичностью, а некоторые там и вовсе не бывают, смещение âûáîðêè неминуемо. В выборке будет представлена только категория студентов, посещающих кафетериé.
А теперь вообразите ситуацию, что вся студенческая братия собралась на стадионе, на футбольном матче за звание чемпиона. Вы решили проинтервьюировать студентов методом случайной выборки. Однако вы старались не вступать в беседу со студентами, одетыми как хиппи, поскольку чувствовали, что они не отнесутся к проведению исследований серьезно. Точно так же вы не стали интервьюировать членов университетских братств и женских клубов, так как считаете, что их мнение не отображает мнения “обычного” студента. Систематическое исключение этих лиц из проведения исследований нарушает принцип случайного отбора и влечет за собой значительное смещение результатов исследования.
Подводя итоги, можно утверждать, что смещения при отборе препятствуют успешному проведению исследований и приведут, скорее всего, к неверным выводам о совокупности, из которой извлекается выборка. Таким образом, процесс планирования выборки должен включать явное обсуждение возможностей возникновения смещений, а также способов устранения источников потенциального смещения на основе приемов проведения случайного отбора.
Объем случайной выборки
Объем выборки непосредственно влияет на степень уверенности обобщений, сделанных на основе выборки. Обычно более крупные по объему выборки обеспечивают большую уверенность в сделанных оценках и их обобщении на генеральную совокупность. Но возрастание уверенности не находится в строгой линейной зависимости от увеличения объема выборки. Для достижения совсем небольшого прироста уверенности приходится довольно значительно увеличивать объем выборки. Следовательно, целью определения размера выборки является определение такого ее минимального объема, который бы обеспечил желаемую степень уверенности в оценках характеристик генеральной совокупности.
Понятие уверенности в оценках и обобщениях, сделанных на основе выборки, выражается с помощью доверительного интервалаи доверительного уровня. Доверительный интервал — это числовой интервал, который между верхней и нижней границами содержит с известной вероятностью значение параметра в генеральной совокупности. Например, часто приходится читать или слышать о том, что “80% опрошенного взрослого населения согласны с тем, что необходимо внести существенные изменения в налоговое законодательство. Доверительный интервал составляет ±2%”. Это означает, что реальный процент отдавших свои голоса в пользу этого заявления находится в интервале 78–82%. Доверительный уровень — это математическое выражение нашей уверенности в том, что параметр генеральной совокупности находится в пределах доверительного интервала. Например, доверительный уровень, составляющий 95%, означает, что существует 95%-ная уверенность в том, что интересующий нас параметр генеральной совокупности находится в пределах установленного в исследовании доверительного интервала.
Объем выборки определяется, исходя из доверительных интервалов и уровней. Чем большую точность оценки необходимо получить, тем больший объем выборки требуется. Таким образом, наиболее важным шагом при определении объема выборки является решение о желаемом доверительном уровне и интервале. Как только это решение будет принято, можно использовать один из способов определения соответствующего объема выборки.
Объем выборки при оценке долей. Если результаты опроса представляются в виде долей (процентов), для определения соответствующего объема выборки можно воспользоваться таблицей, аналогичной табл. 8.3. Вся информация, содержащаяся в данной таблице, составлена на основе 95%-ного доверительного уровня. Для пользования этой таблицей нужно иметь некоторую оценку изучаемой доли. Например, предположим, что для проведения исследований вы разработали три альтернативных вопроса, требующих ответа “согласен–не согласен”. На первый из вопросов вы надеетесь получить утвердительный ответ 10% выборки, на второй — 20%, на третий — 85%. К тому æå предположим, что требуется обеспечить узкий доверительный интервал, составляющий не более чем ±3% для каждого из трех вопросов в отдельности.
Таблица 8.3. Доверительные интервалы для различных объемов выборки и ожидаемой доли (доверительный уровень равен 95%)
| Ожидаемая доля | ||||||||||
| Объем выборки, чел. | 5% или 95% | 10% или 90% | 15% или 85% | 20% или 80% | 25% или 75% | 30% или 70% | 35% или 65% | 40% или 60% | 45% или 55% | 50% |
| 4,4 | 6,0 | 7,1 | 8,0 | 8,7 | 9,2 | 9,2 | 9,5 | 9,8 | 10,0 | |
| 3,1 | 4,7 | 5,0 | 5,7 | 6,1 | 6,5 | 6,7 | 6,9 | 7,0 | 7,2 | |
| 2,5 | 3,5 | 4,2 | 4,6 | 5,0 | 5,3 | 5,5 | 5,7 | 5,7 | 5,8 | |
| 2,2 | 3,0 | 3,6 | 4,0 | 4,3 | 4,6 | 4,8 | 4,9 | 5,0 | 5,0 | |
| 1,9 | 3,0 | 3,2 | 3,6 | 3,9 | 4,1 | 4,3 | 4,4 | 4,5 | 4,5 | |
| 1,8 | 2,5 | 2,9 | 3,3 | 3,5 | 3,7 | 3,9 | 4,0 | 4,0 | 4,1 | |
| 1,6 | 2,3 | 2,7 | 3,0 | 3,3 | 3,5 | 3,6, | 3,7 | 3,8 | 3,8 | |
| 1,5 | 2,2 | 2,5 | 2,8 | 3,1 | 3,2 | 3,4 | 3,5 | 3,5 | 3,5 | |
| 1,4 | 2,0 | 2,4 | 2,7 | 2,9 | 3,1 | 3,2 | 3,3 | 3,3 | 3,3 | |
| 1,4 | 1,9 | 2,3 | 2,5 | 2,7 | 2,9 | 3,0 | 3,1 | 3,1 | 3,2 | |
| 1,1 | 1,5 | 1,8 | 2,0 | 2,2 | 2,4 | 2,5 | 2,5 | 2,6 | 2,6 | |
| 1,0 | 1,3 | 1,6 | 1,8 | 1,9 | 2,0 | 2,1 | 2,2 | 2,2 | 2,2 | |
| 0,8 | 1,1 | 1,3 | 1,5 | 1,6 | 1,7 | 1,7 | 1,8 | 1,8 | 1,8 | |
| 0,6 | 0,8 | 1,0 | 1,1 | 1,2 | 1,3 | 1,3 | 1,4 | 1,4 | 1,4 |
Из табл. 8.3 видно, что при доверительном интервале со значением не более чем ±3% при ожидаемой доле утвердительных ответов:
· 10% — объем выборки должен составлять 400;
· 20% — объем выборки должен составлять 700;
· 85% — объем выборки должен составлять около 600.
Таким образом, окончательный объем выборки при данных значениях должен составлять 700 человек (наибольший из трех требуемых объемов выборки).
Бывают случаи, когда необходимо задать другой доверительный уровень. Следовательно, примером, приведенным в табл. 8.3, руководствоваться нельзя. В этом случае объем выборки можно определить по формуле:
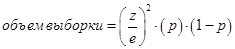 ,
,
где z — z-балл, соответствующий требуемому доверительному уровню, а e — желаемый доверительный интервал. Z-баллы для различных доверительных уровней приведены в таблице.
| Доверительный уровень, % | Z-балл |
| 2,57 | |
| 1,96 | |
| 1,64 |
(Получение z-баллов и доверительных уровней более подробно рассматривается в главе 16.) Представьте, например, следующую ситуацию. Вы обратились к группе респондентов с вопросом: “Знакомы ли вы с рекламой офисного оборудования фирмы Lanier?”, ожидая получить утвердительный ответ от 35% опрашиваемых. Кроме того, вам необходимо на 99% быть уверенными в том, что действительная доля положительных ответов будет находиться в пределах ±2%. Требуемый объем выборки при заданном доверительном уровне получается следующим образом:
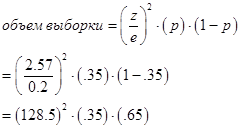
Объем выборки велик, так как доверительный уровень и доверительный интервал задают высокий уровень точности. Однако объем выборки будет гораздо меньшим, если доверительный интервал возрастет до ±4%, а доверительный уровень снизится до 95%:
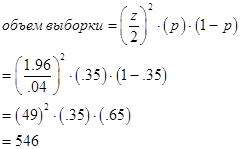
Рис. 8.2. Зависимость между объемом выборки и доверительным уровнем для трех значений ожидаемой ответной реакции при 95%-ном доверительном уровне
Табл. 8.3 также демонстрирует зависимость между доверительными интервалами и объемом выборки. Если полагать, что доверительный уровень имеет постоянную величину, то чтобы уменьшить доверительный интервал вдвое, объем выборки следует увеличить вчетверо. Например, при ожидаемой доле в 20% выборка из 100 участников обеспечивает доверительный интервал ±8%, выборка из 400 — ±4%, а выборка из 1600 участников — ±2%. Зависимость между точностью (выражающейся в меньших доверительных интервалах) и объемом выборки показана на рис. 8.2. Как видим, точность значительно увеличивается при небольшом увеличении объема выборки (приблизительно до 1000 участников), однако увеличение точности существенно замедляется, если объем выборки превышает 1000 участников. Вот почему при проведении большей части потребительских, маркетинговых и рекламных исследовательских работ выборка редко превышает 1000 участников[9].
Вычисление объема выборки в случае, когда оценивается среднее значение. Можно также определить объем выборки, если требуется оценить среднее значение в генеральной совокупности. В этих случаях, кроме указания доверительного уровня и доверительного èíòåðâàëà, необходимо располагать оценкой изменчивости изучаемого признака. (Мерой изменчивости переменной является среднеквадратическое (стандартное) отклонение. В главе 15 подробно рассматривается вычисление и интерпретация этой меры.) Поскольку значение среднеквадратического отклонения в генеральной совокупности редко бывает известно, его можно оценить одним из следующих трех способов.
1.Воспользуйтесь оценкой среднеквадратического отклонения на основании предыдущих аналогичных исследований, проведенных на той же генеральной совокупности.
2.Проведите небольшое пилотажное исследование; используйте среднеквадратическое отклонение, полученное в пилотажных исследованиях, в качестве оценки среднеквадратического отклонения в генеральной совокупности.
3.Вычислите сумму максимального и минимального значений изучаемой переменной и разделите ее на четыре.
Оценив среднеквадратическое отклонение и определив доверительный интервал и доверительный уровень, оценку объема выборки можно получить по следующей формуле:
 ,
,
где так же, как и в предыдущей формуле, z представляет z-балл, соответствующий конкретному доверительному уровню (взят из приведенной ранее таблицы), а e — желаемый доверительный интервал. Новый член этой формулы, s, является оценкой среднеквадратического отклонения в генеральной совокупности.
Приводим пример, подобный только что рассмотренному. Представьте следующую ситуацию. Вы обратились к группе респондентов с просьбой: “Дайте, пожалуйста, оценку правдоподобия рекламы офисного оборудования фирмы Lanier по шкале от одного до пяти”. Вы хотите на 95% быть уверенными в том, что истинное значение среднего рейтинга в генеральной совокупности будет находиться в пределах ±0,2 от среднего значения в выборке. Оценка среднеквадратического отклонения получена путем суммирования экстремальных значений шкалы и деления суммы на четыре, и равна 1,5 (т.е. 5 + 1 : 4 = 1,5). Необходимый объем выборки для заданного желаемого доверительного уровня будет равен 216. Рассчитывается он с помощью формулы:
Дата добавления: 2016-09-20; просмотров: 3521;
