Алгоритм решения дифференциального уравнения с разделяющимися переменными.
1)Если уравнение имеет вид (1), тот производную заменяют на отношение дифференциалов: 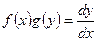 .
.
2)Домножением на 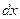 приводим уравнение к виду:
приводим уравнение к виду: 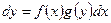 .
.
Замечание: если уравнение имеет вид (2), то просто второе слагаемое переносим в правую часть.
3)С помощью деления или умножения на соответствующие функции собираем все функции, зависящие от х в той части, в которой находится 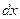 , а все функции, зависящие от у там, где находится
, а все функции, зависящие от у там, где находится 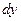 .
.
(1)  (2)
(2) 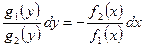
Переменные х и у оказались разделенными знаком равенства (отсюда название уравнения).
Раз дифференциалы, находящиеся в левой и правой части уравнения одинаковы, то одинаковы будут и неопределенные интегралы от левой и правой части.
4)(1) 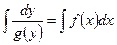 (2)
(2) 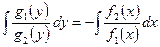 .
.
5)Вычисляя интегралы получаем общий интеграл уравнения: 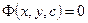 .
.
Пример: найти общее решение дифференциального уравнения, найти частное решение по начальным данным, построить интегральную кривую, соответствующую частному решению.
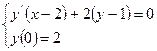
1)
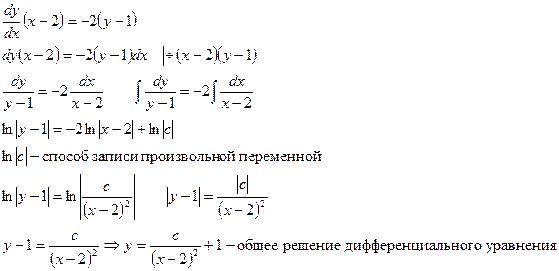
2) подставим в общее решение начальное условие
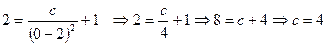
подставим найденное значение произвольной постоянной и получим частное решение:
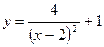 .
.
3)
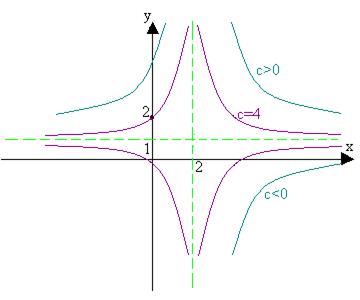
Замечание: в алгоритме решения при переходе от пункта 2 к пункту 3 выполнялось деление на 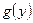 . Если при некотором значении y = b функция
. Если при некотором значении y = b функция 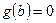 , то в этой точке деление выполнять нельзя и легко видеть, что y = b является решением дифференциального уравнения.
, то в этой точке деление выполнять нельзя и легко видеть, что y = b является решением дифференциального уравнения.
Аналогичное замечание можно сделать и для того случая, когда уравнение представлено в виде (2).
Замечание: уравнения с разделяющимися переменными наиболее простые и одновременно важные среди дифференциальных уравнений первого порядка, поскольку к такому виду сводятся многие другие дифференциальные уравнения.
Пример: уравнение вида 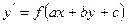 сводится к уравнению с разделяющимися переменными заменой:
сводится к уравнению с разделяющимися переменными заменой:
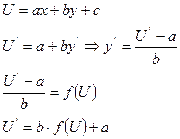
Пример: 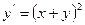
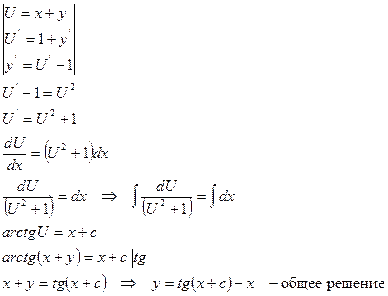
Дата добавления: 2016-06-24; просмотров: 4796;
