Линейные однородные дифференциальные уравнения второго порядка.
Определение:линейным однородным дифференциальным уравнением второго порядка будем называть уравнение вида: 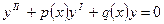 , где
, где 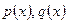 - непрерывные функции.
- непрерывные функции.
Определение:функции 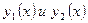 будем называть линейно зависимыми, если существуют коэффициенты
будем называть линейно зависимыми, если существуют коэффициенты 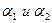 , не все равные нулю, такие, что:
, не все равные нулю, такие, что: 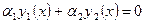 .
.
Определение:функции 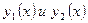 называются линейно независимыми, если выполнение равенства
называются линейно независимыми, если выполнение равенства 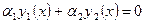 возможно лишь в случае
возможно лишь в случае 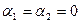 .
.
Замечание:эти определения линейной зависимости и линейной независимости функций естественным образом обобщаются на произвольное число функций.
Если функции 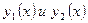 линейно зависимы, то одну из них можно выразить через другую, а именно
линейно зависимы, то одну из них можно выразить через другую, а именно 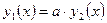 , и наоборот.
, и наоборот.
Пример:покажем, что функции 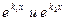 линейно независимы, если
линейно независимы, если 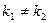 .
.
Пусть 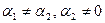 , и при этом выполнено равенство:
, и при этом выполнено равенство:
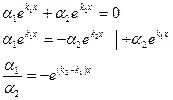
Это равенство никогда не может быть тождественно выполнено, поскольку в левой части постоянная величина, а в правой части, в силу 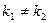 , находится функция, экспоненциально зависящая от переменной х.
, находится функция, экспоненциально зависящая от переменной х.
Теорема:если 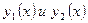 - это два линейно независимые решения уравнения
- это два линейно независимые решения уравнения 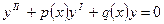 , то общее решение этого дифференциального уравнения может быть представлено в виде:
, то общее решение этого дифференциального уравнения может быть представлено в виде: 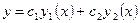 .
.
Покажем, что 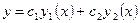 является решением дифференциального уравнения:
является решением дифференциального уравнения:
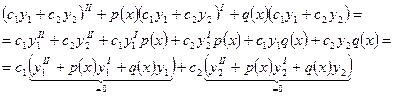
Выражения в скобках равны нулю, поскольку 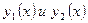 - это решения исходного уравнения, следовательно сумма равна нулю. А поскольку решение содержит две произвольные постоянные
- это решения исходного уравнения, следовательно сумма равна нулю. А поскольку решение содержит две произвольные постоянные 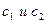 - это решение является общим.
- это решение является общим.
Замечание:можно доказать также, что у дифференциального уравнения 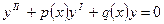 любое решение имеет вид
любое решение имеет вид 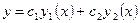 .
.
Дата добавления: 2016-06-24; просмотров: 803;
