Однородные дифференциальные уравнения.
Определение: однородной функцией степени n называется функция 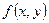 , обладающая следующим свойством:
, обладающая следующим свойством: 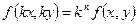 .
.
Пример:
1) 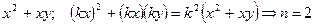 .
.
2) 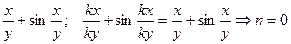 .
.
Определение: однородными дифференциальными уравнениями будем называть дифференциальные уравнения следующего вида: 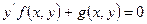 , где
, где 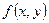 и
и 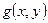 - это однородные функции одинаковой степени.
- это однородные функции одинаковой степени.
Отношение двух однородных функций одинаковой степени всегда можно представить в виде функции, зависящей от 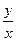 , т.е.
, т.е. 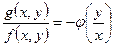 .
.
Для этого достаточно разделить функцию 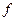 и функцию
и функцию 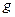 на
на 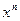 , где n – степень однородной функции. Тогда однородное уравнение принимает вид:
, где n – степень однородной функции. Тогда однородное уравнение принимает вид: 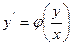 . Это уравнение сводится к уравнению с разделяющимися переменными относительно новой переменной U, которая выводится равенством y = Ux, производная при этом
. Это уравнение сводится к уравнению с разделяющимися переменными относительно новой переменной U, которая выводится равенством y = Ux, производная при этом 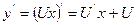 . Получаем уравнение:
. Получаем уравнение: 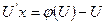 .
.
Пример: найти общее решение дифференциального уравнения 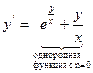 .
.
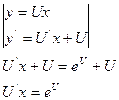
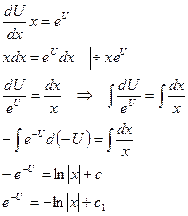
Возьмем логарифм от обеих частей уравнения:
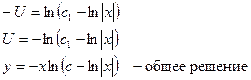
Замечание: иногда удобнее вводить другую переменную в однородных уравнениях, а именно считать независимой переменной у, зависимой переменной х и новую переменную вводить равенством 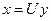 , а производную
, а производную 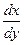 равенством
равенством 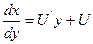 (функцию U рассматривать как функцию
(функцию U рассматривать как функцию 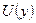 ).
).
Уравнения вида 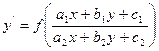 сводятся к однородным в тех случаях, когда определитель
сводятся к однородным в тех случаях, когда определитель 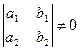 . В этом случае от переменных х и у переходят к новым переменным U и V по формулам:
. В этом случае от переменных х и у переходят к новым переменным U и V по формулам: 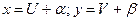 , где числа α и β находятся из решения системы:
, где числа α и β находятся из решения системы:
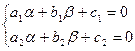 .
.
Если определитель 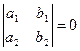 , то вводя новую переменную
, то вводя новую переменную 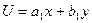 вместо у, получим относительно U уравнение с разделяющимися переменными.
вместо у, получим относительно U уравнение с разделяющимися переменными.
Пример:
Найти общее решение уравнения: 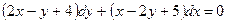 .
.
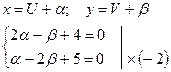
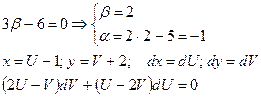
получили однородное уравнение, которое решается заменой:
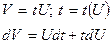
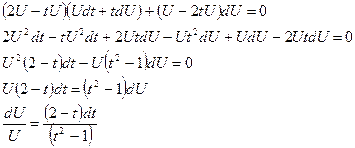
Это уравнение с разделяющимися переменными.
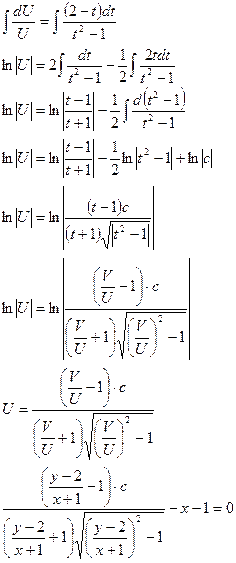
Дата добавления: 2016-06-24; просмотров: 1235;
