Дифференциальные уравнения
II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ФИЛЬТРАЦИИ ЖИДКОСТЕЙ И ГАЗОВ
Общие положения.
Процессы, происходящие в нефтяных и газовых пластах при разработке нефтяных и газовых месторождений, существенно зависят от времени, т.е. являются нестационарными. Характеристики движения жидкости или газа - давление, скорость фильтрации и т.п. изменяются от точки к точке продуктивного пласта и образуют нестационарное поле давлений, скоростей фильтрации и т.п . Задачи нестационарной фильтрации жидкости или газа в пласте решаются методом математической физики; для этого составляются и интегрируются соответствующие дифференциальные уравнения.
К числу дифференциальных уравнений относятся:
1. дифференциальные уравнения движения жидкости или газа;
2. уравнение баланса массы в элементе пористой среды - уравнение неразрывности (сплошности) фильтрационного потока.
Дополнительно к дифференциальным уравнениям вводятся уравнения состояния флюида и пористой среды, определяемые параметрами 
.
В итоге получаем замкнутую систему уравнений, т.е число уравнений в системе равно числу неизвестных функций, характеризующих рассматриваемый фильтрационный процесс и подлежащих определению.
Для получения решения системы уравнений должны быть заданы начальные (при t=0) и краевые (граничные) условия - на границах пласта. При этом заметим, что фильтрация представляет собой очень медленный процесс и изменение температуры флюида в ходе движения (вследствие наличия сопротивления и расширения вещества) успевает компенсироваться теплообменом с окружающими горными породами. Поэтому считаем, что температура флюида равна температуре пористой среды и неизменна, т.е. Тф=Тс=Т=const; это означает, что фильтрация считается изотермическим процессом.
В результате интегрирования полученных итоговых дифференциальных уравнений фильтрации получаем закон распределения давления, а, следовательно, и скорости фильтрации по всему пласту в любой момент времени, т.е. Р=Р(x,y,z,t); ux=ux(x,y,z,t); uу=uу(x,y,z,t), uz=uz(x,y,z).
Если принять жидкость несжимаемой (r=const) в недеформируемой пористой среде (m=const,k=const) – самый упрощенный случай, то число искомых функций ограничится этими четырьмя параметрами (Р,Vx,Vy,Vz).
Если предполагается фильтрация сжимаемого флюида в сжимаемой пористой среде, предстоит еще дополнительно определить значения параметров r,m,k,m как функции координат и времени. В этом случае имеем восемь уравнений - дифференциальных и конечных- для определения восьми характеристик фильтрационного потока, жидкости (газа) и пористой среды. Аналитическое решение системы диф. уравнений в этом (общем) случае невозможно; необходимо численное решение с применением ЭВМ.
Дифференциальные уравнения
Движения флюида
Дифференциальные уравнения движения флюида получаются непосредственно из закона Дарси для трубки тока переменного сечения (рис.4)
, (2.1)
где Р - приведенное давление, Р=Р(S,t) .
Или в векторной форме:
. (2.2)
При этом предполагается изотропность пористой среды, т.е. предполагается постоянство проницаемости k по всем направлениям в окрестности рассматриваемой точки.
Представим вектор скорости фильтрации через составляющие по координатным осям:
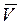= Vx*`i + Vy*`j +Vz*`k (а)
Дата добавления: 2016-06-13; просмотров: 2226;