Выбор формы уравнения регрессии.

Для построения уравнения множественной регрессии чаще используются следующие функции

1. линейная: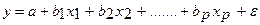

2. степенная: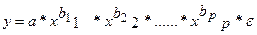

3. экспоненциальная: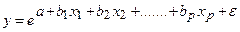

4. гипербола: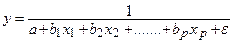

В виду четкой интерпретации параметров наиболее широко используются линейная и степенная функции. В линейной множественной регрессии параметры при Х называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне.

Пример. Предположим, что зависимость расходов на продукты питания по совокупности семей характеризуется следующим уравнением:

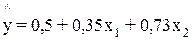
где у – расходы семьи за месяц на продукты питания, тыс.руб.;

х₁ – месячный доход на одного члена семьи, тыс.руб.;

х₂ – размер семьи, человек.

Анализ данного уравнения позволяет сделать выводы – с ростом дохода на одного члена семьи на 1 тыс. руб. расходы на питание возрастут в среднем на 350 руб. при том же среднем размере семьи. Иными словами, 35% дополнительных семейных расходов тратится на питание. Увеличение размера семьи при тех же ее доходах предполагает дополнительный рост расходов на питание на 730 руб. Параметр а не подлежит экономической интерпретации.

При изучении вопросов потребления коэффициенты регрессии рассматривают как характеристики предельной склонности к потреблению. Например, если функции потребления С_t имеет вид:

С_t = a+b₀ R_t + b₁ R_t-1 +e,

то потребление в период времени t зависит от дохода того же периода R_t и от дохода предшествующего периода R_t-1. Соответственно коэффициент b₀ обычно называют краткосрочной предельной склонностью к потреблению. Общим эффектом возрастания как текущего, так и предыдущего дохода будет рост потребления на b= b₀ + b₁. Коэффициент b рассматривается здесь как долгосрочная склонность к потреблению. Так как коэффициенты b₀ и b₁ >0, то долгосрочная склонность к потреблению должна превосходить краткосрочную b₀. Например, за период 1905 – 1951 гг. (за исключением военных лет) М.Фридман построил для США следующую функцию потребления: С_t = 53+0,58 R_t+0,32 R_t-1 с краткосрочной предельной склонностью к потреблению 0,58 и с долгосрочной склонностью к потреблению 0,9.

Функция потребления может рассматриваться также в зависимости от прошлых привычек потребления, т.е. от предыдущего уровня потребления

С_t-1:

С_t = a+b₀ R_t +b₁ С_t-1 +e,

В этом уравнении параметр b₀ также характеризует краткосрочную предельную склонность к потреблению, т.е. влияние на потребление единичного роста доходов того же периода R_t. Долгосрочную предельную склонность к потреблению здесь измеряет выражение b₀/(1- b₁).

Так, если уравнение регрессии составило:

С_t = 23,4+0,46 R_t +0,20 С_t-1 +e,

то краткосрочная склонность к потреблению равна 0,46, а долгосрочная – 0,575 (0,46/0,8).

В степенной функции 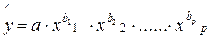коэффициенты b_j являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1% при неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и потребления.

Предположим, что при исследовании спроса на мясо получено уравнение:

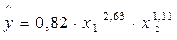
где у – количество спрашиваемого мяса

х₁ – цена

х₂ – доход.

Следовательно, рост цен на 1% при том же доходе вызывает снижение спроса на мясо в среднем на 2.63%. Увеличение дохода на 1% обусловливает при неизменных ценах рост спроса на 1.11%.

В производственных функциях вида:

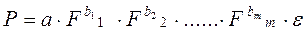
где P – количество продукта, изготавливаемого с помощью m производственных факторов (F₁, F₂, ……F_m).

b – параметр, являющийся эластичностью количества продукции по отношению к количеству соответствующих производственных факторов.

Экономический смысл имеют не только коэффициенты b каждого фактора, но и их сумма, т.е. сумма эластичностей: В = b₁ +b₂+……+b_m. Эта величина фиксирует обобщенную характеристику эластичности производства. Производственная функция имеет вид

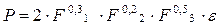
где Р – выпуск продукции

F₁ – стоимость основных производственных фондов

F_2­ ­ - отработано человеко-дней

F₃ – затраты на производство

Эластичность выпуска по отдельным факторам производства составляет в среднем 0,3% с ростом F₁ на 1% при неизменном уровне других факторов; 0,2% - с ростом F_2­ ­ на 1% также при неизменности других факторов производства и 0,5% с ростом F₃ на 1% при неизменном уровне факторов F₁ и F₂. Для данного уравнения В = b₁ +b₂+b₃ = 1. Следовательно, в целом с ростом каждого фактора производства на 1% коэффициент эластичности выпуска продукции составляет 1%, т.е. выпуск продукции увеличивается на 1%, что в микроэкономике соответствует постоянной отдаче на масштаб.

При практических расчетах не всегда 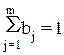. Она может быть как больше, так и меньше 1. В этом случае величина В фиксирует приближенную оценку эластичности выпуска с ростом каждого фактора производства на 1% в условиях увеличивающейся (В>1) или уменьшающейся (В<1) отдачи на масштаб.

Так, если 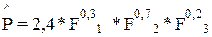, то с ростом значений каждого фактора производства на 1% выпуск продукции в целом возрастает приблизительно на 1.2%.

При оценке параметров модели по МНК мерой (критерием) количества подгонки эмпирической регрессионной модели к наблюдаемой выборке служит сумма квадратов ошибок (остатков).

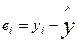
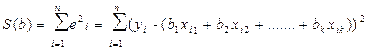
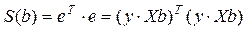где е = (e1,e2,…..e_n)^T;

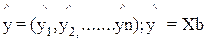
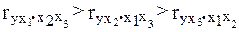
Для уравнения применили равенство:

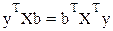
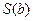- скалярная функция

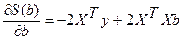
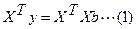
Система нормальных уравнений (1) содержит k линейных уравнений относительно k неизвестных i = 1,2,3……k

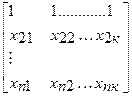
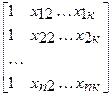
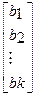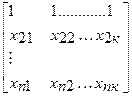
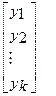= (2)

Перемножив (2) получим развернутую форму записи систем нормальных уравнений

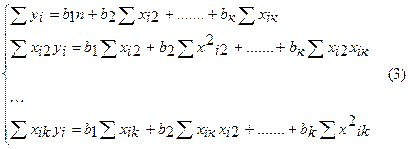
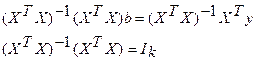
Оценка коэффициентов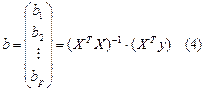

Стандартизированные коэффициенты регрессии, их интерпретация. Парные и частные коэффициенты корреляции. Множественный коэффициент корреляции. Множественный коэффициент корреляции и множественный коэффициент детерминации. Оценка надежности показателей корреляции.

Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии.

Так, для уравнения 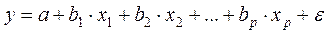система нормальных уравнений составит:

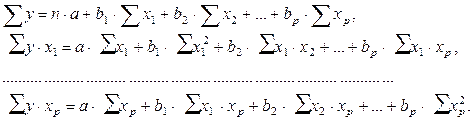
Ее решение может быть осуществлено методом определителей:

, ,…, ,

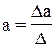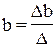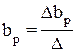где D – главный определитель системы;

Dа, Db₁, …, Db_p – частные определители.

При этом

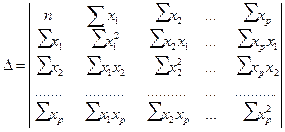
а Dа, Db₁, …, Db_p получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.

Возможен и иной подход в определении параметров множественной регрессии, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:

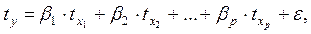
где 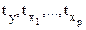- стандартизованные переменные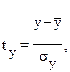 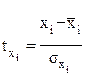, для которых среднее значение равно нулю 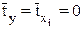, а среднее квадратическое отклонение равно единице: ;

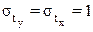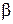- стандартизованные коэффициенты регрессии.

Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных вида

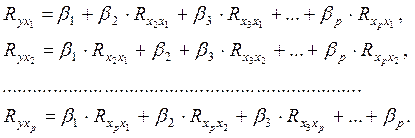
Решая ее методом определителей, найдем параметры – стандартизованные коэффициенты регрессии (b-коэффициенты).

Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результат, если соответствующий фактор х_i изменится на одну сигму при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии b_I сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.

Пример. Пусть функция издержек производства у (тыс. руб.) характеризуется уравнением вида

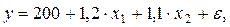
где х₁ – основные производственные фонды;

х₂ – численность занятых в производстве.

Анализируя его, мы видим, что при той же занятости дополнительный рост стоимости основных производственных фондов на 1 тыс. руб. влечет за собой увеличение затрат в среднем на 1,2 тыс. руб., а увеличение численности занятых на одного человека способствует при той же технической оснащенности предприятий росту затрат в среднем на 1,1 тыс. руб. Однако это не означает, что фактор х₁ оказывает более сильное влияние на издержки производства по сравнению с фактором х₂. Такое сравнение возможно, если обратиться к уравнению регрессии в стандартизованном масштабе. Предположим, оно выглядит так:

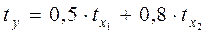
Это означает, что с ростом фактора х₁ на одну сигму при неизменной численности занятых затрат на продукцию увеличиваются в среднем на 0,5 сигмы. Так как b₁ < b₂ (0,5 < 0,8), то можно заключить, что большее влияние оказывает на производство продукции фактор х₂, а не х₁, как кажется из уравнения регрессии в натуральном масштабе.

В парной зависимости стандартизованный коэффициент регрессии есть не что иное, как линейный коэффициент корреляции r_xy. Подобно тому, как в парной зависимости коэффициент регрессии и корреляции связаны между собой, так и в множественной регрессии коэффициенты «чистой» регрессии b_i связаны со стандартизованными коэффициентами регрессии b_i, а именно:

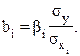(3.1)

Это позволяет от уравнения регрессии в стандартизованном масштабе

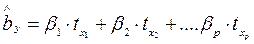(3.2)

переход к уравнению регрессии в натуральном масштабе переменных:

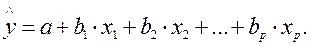
Параметр а определяется как

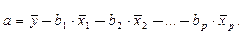(3.3)

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов – из модели исключаются факторы с наименьшим значением b_j.

Компьютерные программы построения уравнения множественной регрессии в зависимости от использованного в них алгоритма решения позволяют получить либо только уравнение регрессии для исходных данных, либо, кроме того, уравнение регрессии в стандартизованном масштабе.

При нелинейной зависимости признаков, приводимой к линейному виду, параметры множественной регрессии также определяются МНК с той лишь разницей, что он используется не к исходной информации, а к преобразованным данным. Так, рассматривая степенную функцию

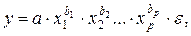
мы преобразовываем ее в линейный вид:

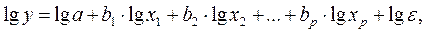
где переменные выражены в логарифмах.

Далее обработка МНК та же, что и описана выше: строится система нормальных уравнений и определяются параметры lga, b₁, b₂, … b_p. Потенцируя значение lga, найдем параметр а и соответственно общий вид уравнения степенной функции.

Поскольку параметры степенной функции представляют собой коэффициенты эластичности, то они сравнимы по разным факторам.

Пример. При исследовании спроса на масло получено следующее уравнение:

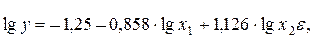где

у – количество масла на душу населения (кг);

х₁ – цена (руб.)

х₂ – доход на душу населения (тыс. руб.).

Анализируя уравнение, видим, что с ростом цены на 1% при том же доходе спрос снижается в среднем на 0,858%, а рост дохода на 1% при неизменных ценах вызывает увеличение спроса в среднем на 1,126%. В виде степенной функции данное уравнение примет вид:

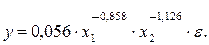
При других нелинейных функциях методика оценки параметров МНК осуществляется так же. В отличие от предыдущих функций параметры более сложных моделей не имеют четкой экономической интерпретации: они не являются показателями силы связи и ее эластичности. Это не исключает возможности их применения, но делает их менее привлекательными в практических расчетах.