Классическая модель множественной линейной регрессии.

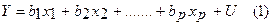
y – регрессанд

x_i – регрессоры

u – случайная составляющая.

Модель множественной регрессии является обобщением модели парной регрессии на многомерный случай.

Независимые переменные (х) предполагаются не случайными (детерминированными) величинами.

Переменная х₁ = x_i1 = 1 называется вспомогательной переменной для свободного члена и еще в уравнениях она называется параметром сдвиги.

«y» и «u» в (2) являются реализациями случайной величины.

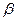- называется также параметром сдвига.

Для статистической оценки параметров регрессионной модели необходим набор (множество) данных наблюдений независимых и зависимых переменных. Данные могут быть представлены в виде пространственных данных или временных рядов наблюдений. Для каждого из таких наблюдений согласно линейной модели можно записать:

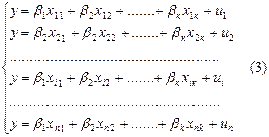
Векторно-матричная запись системы (3).

Введем следующие обозначения:

вектор-столбец независимой переменной (регрессанда)

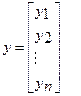размерность матрицы (n·1)

Матрица наблюдений независимых переменных (регрессоров):

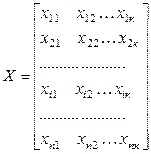размер (n·k)

Вектор-столбец параметров:

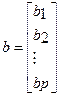
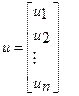
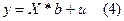- матричная запись системы уравнений (3). Она проще и компактнее.