Множественная корреляция

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации.

Показатель множественной корреляции характеризует тесноту рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

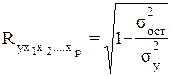, (3.6)

где s²_y – общая дисперсия результативного признака;

s_ост² – остаточная дисперсия для уравнения у = ¦(х_1,х₂,….,x_p).

Методика построения индекса множественной корреляции аналогична построению индекса корреляции для парной зависимости. Границы его изменения те же: от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:

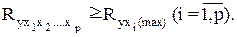
При правильном включении факторов в регрессионной анализ величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции (различия в третьем, четвертом знаках). Отсюда ясно, что, сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того фактора. Так, если y рассматривается как функция x и z и получен индекс множественной корреляции R_yzx = 0,85, а индексы парной корреляции при этом были R_yx = 0,82 и R_yz = 0,75, то совершенно ясно, что уравнение парной регрессии у = ¦(х) охватывало 67,2% колеблемости результативного признака под влиянием фактора x а дополнительное анализ фактора z увеличило долю объясненной вариации до 72,3%, т.е. уменьшилась доля остаточной вариации на 5,1 проц. Пункта (с 32,8 до 27,7 %).

Расчет индекса множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии:

.

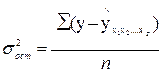Можно пользоваться следующей формулой индекса множественной корреляции:

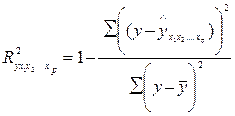. (3.7)

При линейной зависимости признаков формула индекса корреляции может быть представлена следующим выражением:

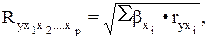(3.8)

где 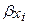- стандартизованные коэффициенты регрессии;

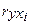- парные коэффициенты корреляции результата с каждым фактором.

В справедливости данной формулы можно убедиться, если обратиться к линейному уравнению множественной регрессии в стандартизованном масштабе и определить для его индекс множественной корреляции как

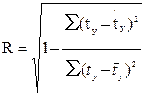(3.9)

Или, что то же самое,

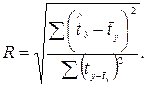(3.10)

В формуле (3.10) числитель подкоренного выражения представляет собой факторную сумму квадратов отклонений для стандартизованных переменных: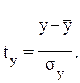

Поскольку 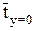и , и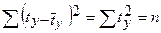ндекс множественной корреляции для линейной уравнения в стандартизованном масштабе можно записать в виде

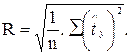(3.11)

Подставим в эту формулу выражение 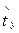через

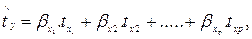
получим:

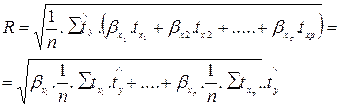
Так как 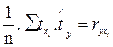то получим формулу индекса множественной корреляции следующего вида (3.8):

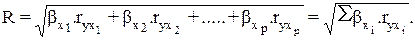
Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции, или, что то же самое, совокупного коэффициента корреляции.

Возможно также при линейной зависимости определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции:

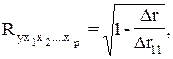(3.12)

где Dr – определитель матрицы парных коэффициентов корреляции;

Dr₁₁ – определитель матрицы межфакторной корреляции.

Для уравнения 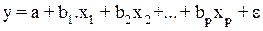определитель матрицы коэффициентов парной корреляции примет вид:

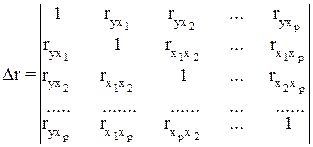. (3.13)

Определитель более низкого порядка r₁₁ остается, когда вычеркиваются из матрицы коэффициентов парной корреляции первый столбец и первая строка, что и соответствует матрице коэффициентов парной корреляции между факторами:

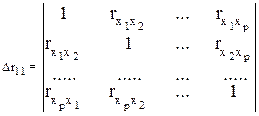. (3.14)

Как видом, величина множественного коэффициента корреляции зависит не только от корреляции результата с каждым из факторов, но и от межфакторной корреляции. Рассмотренная формула позволяет определить совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции.

При трех переменных для двухфакторного уравнения регрессии данная формула совокупного коэффициента корреляции легко приводится к следующему виду:

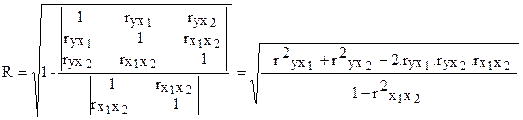(3.15)

Индекс множественной корреляции равен совокупному коэффициенту корреляции не только при линейной зависимости рассматриваемых признаков. Тожественность этих показателей, как и а парной регрессии, имеет место и для криволинейной зависимости, нелинейной по переменным. Так, если фирмы модель прибыли у имеет вид

,

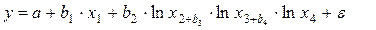где х₁ – удельные расходы на рекламу;

х₂ - капитал фирмы;

х₃ – доля продукции фирмы в общем объеме продаж данной группы товаров по региону;

х₄ – процент увеличения объема продаж фирмы по сравнению с предыдущим годом.

Тогда независимо от того; что фактор х₁ задан линейно, а факторы х₂, х_3, х₄ – в логарифмах, оценка тесноты связи может быть произведена с помощью линейного коэффициента множественной корреляции. Так, если рассматриваемая модель в стандартизованном виде оказалась следующей:

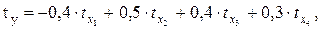
а парные коэффициенты корреляции прибыли с каждым из ее факторов составили

,

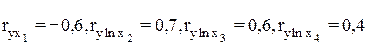то коэффициент множественной детерминации окажется равным:

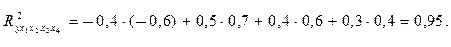
Тот же результат даст и индекс множественной детерминации, определенный через соотношение остаточной и общей дисперсии результативного признака.

Иначе обстоит дело с криволинейной регрессией, нелинейной по оцениваемым параметрам. Предположим, что рассматривается производственная функция Кобба – Дугласа:

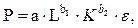
где P – объем продукции;

L – затраты труда;

K – величина капитала;

b₁ + b₂ = 1.

Логарифмируя ее, получим линейное в логарифмах уравнение

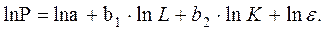
Оценив параметры этого уравнения по МНК, можно найти теоретические значения объема продукции 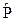и соответственно остаточную сумму квадратов 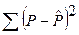, которая используется в расчете индекса детерминации (корреляции):

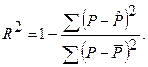
Однако при этом нельзя забывать, что МНК применяется не к исходным данным продукции, а к их логарифмам. Поэтому в индексе корреляции с общей суммой квадратов 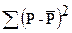сравнивается остаточная дисперсия, которая определена по теоретическим значениям логарифмов продукции: 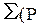– антилогарифм 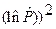, т.е. по 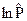путем потенцирования нашли .

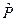В показателях множественной корреляции (индекс и коэффициент) используется остаточная дисперсия, которая имеет систематическую ошибку в сторону преуменьшения, тем более значительную, чем больше параметров определяется в уравнении регрессии при заданном объеме наблюдений n. Если число параметров при x_j равно m и приближается к объеме наблюдений, то остаточная дисперсия будет близка к нулю и коэффициент (индекс) корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной регрессии.

Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумму квадратов 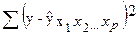делится на число степеней свободы остаточной вариации (n-m-1), а общая сумма квадратов отклонений 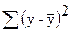- на число степеней свободы в целом по совокупности (n – 1).

Формула скорректированного индекса множественно детерминации имеет вид:

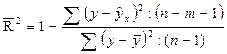, (3.17)

где m – число параметров при переменных х;

n – число наблюдений.

Поскольку 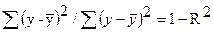, то величину скорректированного индекса детерминации можно представить в виде

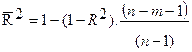(3.18)

Чем больше величина m, тем сильнее различия 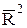и .

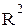Для линейной зависимости признаков скорректированный коэффициент множественной корреляции определяется по той же формуле, что и индекс множественной корреляции, т.е. как корень квадратный из 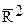. Отличие состоит лишь в том, что в линейной зависимости под m подразумевается число факторов включенных в регрессионную модель, а в криволинейной зависимости m – число параметров при х и их преобразованиях (х², lnx и др.), которое может быть больше числа факторов как экономических переменных. Так, если у = f (x₁, x₂), то для линейной регрессии m=2, а для регрессии вида

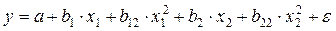
число параметров при х равно 4, т.е. m = 4. При заданном объеме наблюдений при прочих равных условиях с увеличением числа независимых переменных (параметров) скорректированный коэффициент множественной детерминации убывает. Его величина может стать и отрицательной при слабых связях результата с факторами. В этом случае он должен считаться равным нулю. При небольшом числе наблюдений скорректированная величина коэффициента множественной детерминации R² имеет тенденцию переоценивать долю вариации результативного признака, связанную с влиянием факторов, включенных в регрессионную модель.

Пример.Предположим, что при n = 30 для линейного уравнения регрессии с четырьмя факторами R² = 0,7, а с учетом корректировки на число степеней свободы

.

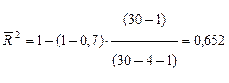Чем больше объем совокупности, по которой исчислена регрессия, тем меньше различаются показатели 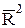и R². Так, уже при n = 50 при том же значении R² и m величина 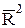составит 0,673.

В статистических пакетах прикладных программ в процедуре множественной регрессии обычно приводится скорректированный коэффициент (индекс) множественной корреляции (детерминации). Величина коэффициента множественной детерминации используется для оценки качества регрессионной модели. Низкое значение коэффициента (индекса) множественной корреляции означает, что в регрессионную модель невключены существенные факторы – с одной стороны, а с другой стороны – рассматриваемая форма связи не отражает реальные соотношения между переменными, включенными в модель. Требуются дальнейшие исследования по улучшению качества модели и увеличению ее практической значимости.

Частная корреляция

Как было показано выше, ранжирование факторов, участвующих в множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии ( 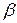- коэффициенты). Эта же цель может быть достигнута с помощью частных коэффициентов корреляции – для линейных связей. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации. Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включения того или иного фактора в модель показывается величиной показателя частной корреляции.

Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.

Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.

Пример. Предположим, что зависимость объема продукции у от затрат труда x₁ характеризуется уравнением

,

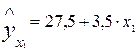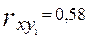
Подставив в это уравнение фактические значения x₁, найдем теоретические величины объема продукции 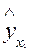и соответствующую величину остаточной дисперсии :

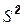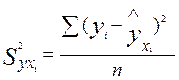
Включив уравнение регрессии дополнительный фактор x₂- теоретическую оснащенность производства, получим уравнение регрессии вида

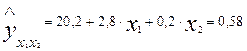
Для этого уравнения остаточная дисперсия, естественно, меньше. Предположим, что 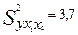, а 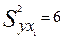. Чем большее число факторов включено в модель, тем меньше величина остаточной дисперсии.

Сокращение остаточно дисперсии за счет дополнительного включения фактора x₂ составит:

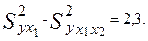
Чем больше доля этого сокращения в остаточной вариации до введения дополнительного фактора, т. е. в 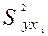, тем теснее связь между y и x₂ при постоянном действии фактора x₁. Корень квадратный из этой величины и есть индекс частной корреляции, показывающий в <<чистом>> виде тесноту связи y с x₂.

Следовательно, чистое влияние фактора x₂ на результат y можно определить как

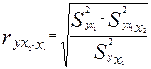(3.19)

Аналогично определяется и чистое влияние на результат фактора x₁:

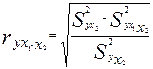(3.20)

Если предположить, что 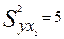, то частные показатели корреляции для уравнения 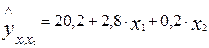составят

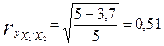
и

Сравнивая полученные результаты, видим, что более сильное воздействие на объем продукции оказывает техническая оснащенность предприятий.

Если выразить остаточную дисперсию через показатель детерминации 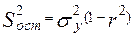, то формула коэффициента частной корреляции примет вид:

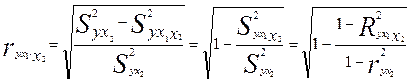(3.21)

Соответственно

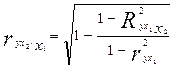(3.22)

Рассмотренные показатели частной корреляции принято называть коэффициентами (индексами) частной корреляции первого порядка, ибо они фиксируют тесноту связи двух переменных при закреплении (элиминировании влияния) одного фактора.

Если рассматривается регрессия с числом факторов 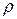, то возможно частные коэффициенты корреляции не только первого, но и второго, третьего, …, ( 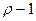) порядка, т. е. влияние фактора x₁ можно оценить при разных условиях независимости действия других факторов:

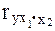-при постоянном действии фактора x₂;

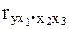-при постоянном действии факторов x₂ и x₃;

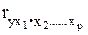-при неизменном действии всех факторов, включенных в уравнение регрессии.

Сопоставление коэффициентов частной корреляции разного порядка по мере увеличения числа включаемых факторов показывает процесс “очищения” зависимости результативного признака с исследуемым фактором.

Например, при изучении зависимости себестоимости добычи угля от объема добычи парный коэффициент корреляции оказался равным -0,75, характеризуя довольно тесную обратную связь признаков. Частный коэффициент корреляции этой зависимости при постоянном влиянии уровня производительности труда составил -0,58 и демонстрирует хотя и достаточную, но уже заметно менее тесную связь себестоимости и объема добычи. Закрепив на постоянном уровне также и размер основных фондов, теснота связи рассматриваемых признаков оказывается еще более низкой, т. е. -0,52.

Хотя частная корреляция разных порядков и может представлять аналитический интерес, в практических исследованиях предпочтение отдают показателям частной корреляции самого высокого порядка, ибо именно эти показатели являются дополнением к уравнению множественной регрессии.

В общем виде при наличии 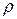факторов для уравнения

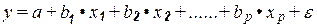
Коэффициент частной корреляции, измеряющий влияние на у фактора x_i при неизменном уровне других факторов, можно определить по формуле

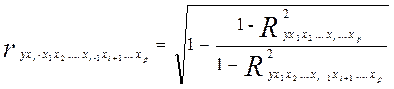(3.23)

Где 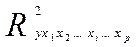- множественный коэффициент детерминации всего комплекса 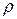факторов с результатом;

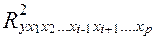- тот же показатель детерминации, но без введения в модель фактора x_i.

При i=1 формула коэффициента частной корреляции примет вид:

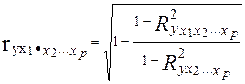(3.24)

Данный коэффициент частной корреляции позволяет измерить тесноту связи между y и x₁ при неизменном уровне всех других факторов, включенных в уравнение регрессии.

Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например, 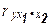- коэффициент частной корреляции первого порядка. Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле

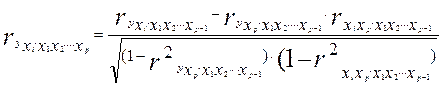
При двух факторах и i=1 данная формула примет вид:

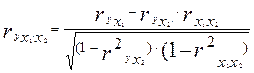
Соответственно при i=2 и двух факторах частный коэффициент корреляции у с фактором x₂ можно определить по формуле

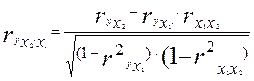
Для уравнения регрессии с тремя факторами частные коэффициенты корреляции второго порядка определяются на основе частных коэффициентов корреляции первого порядка. Так, по уравнению

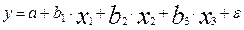
Возможно исчисление трех частных коэффициентов корреляции второго порядка:

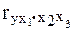
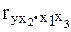
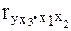
Каждый из которых определяется по рекуррентной формуле.

Например, при i=1 имеем формулу для расчета 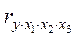, а именно

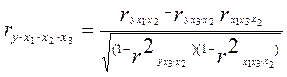
Пример. Предположим, изучается зависимость тиража газеты у от ожидаемого дохода от распродажи газеты x₁, количества персонала редакции x₂, рейтинга газеты среди других газет, распространяемых в регионе x₃. в этом случае матрица парных коэффициентов корреляции составила:

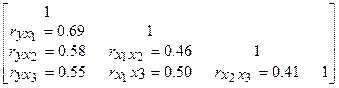
Исходя из этих данных, найдем частные коэффициенты корреляции первого и второго порядка.

Приведем частные коэффициенты корреляции первого порядка зависимости y от x₁ и x₂.

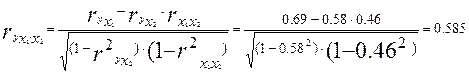
Т.е. при закреплении фактора x₂ на постоянном уровне корреляция y и x₁ оказывается более низкой (0,585 против 0,69);

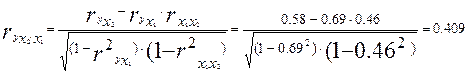
Т. е. при закреплении фактора x₁ на постоянном уровне влияние фактора x₂ на y оказывается менее сильным (0,409 против 0,58);

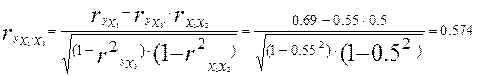
Т. е. при закреплении фактора x₃ на постоянном уровне влияние фактора x₁ на y несколько снизилось по сравнению с парой корреляцией (0,574 против 0,69 ) ввиду некоторой связи факторов x₁ и x₃ ;

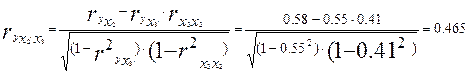
Т. е. при закреплении фактора x₃ на постоянном уровне влияние на у фактора x₂ оказалось несколько менее сильным (0,465 против 0,58);

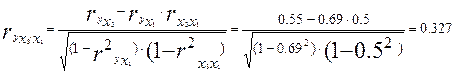
Т.е. корреляция фактора x₃ с y снизилась при фиксированном влиянии на у фактора x₁ (0,55 и 0,327);

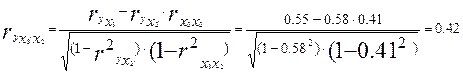
Т.е при закреплении фактора x₂ на постоянном уровне влияние фактора x₃ на у оказалось менее значительным (0,420 и 0,55).

Приведем частные коэффициенты корреляции второго порядка.

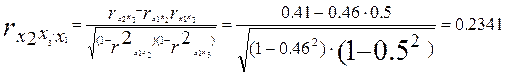
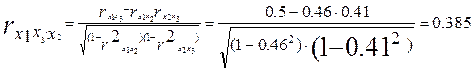
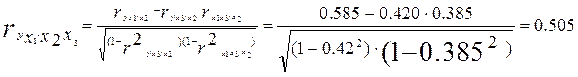
При фиксированном влиянии факторов x₂ и x₃ корреляция у с x₁ оказалась еще меньше, чем при частной корреляции первого порядка (при закреплении фактора x₂): 0,69 ;0,585 и 0,505.

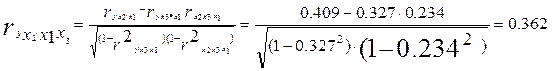
Корреляция фактора x₂ с у снизилась до 0,409 при элиминировании фактора x₁ и до 0,362 при элиминировании двух факторов – x₁ и x₃.

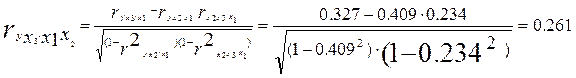
Корреляция у с x₃ снизилась с 0,55 в равной регрессии до 0, 327 при закреплении на постоянном уровне фактора x₁­ и до 0,261 при одновременном закреплении на постоянном уровне факторов x₁ и x₂. Частная корреляция второго порядка зависимости у с факторами x₁,x₂ и x₃ оказалась значительно более низкой – 0,505; 0,362 и 0,261 против 0,69; 0,58 и 0,55 для парной регрессии.

Рассчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от -1 до +1, а по формулам через множественные коэффициенты детерминации – от 0 до 1. сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом. Частные коэффициенты корреляции, подтверждая ранжировку факторов по их воздействию на результат, на основе стандартизованных коэффициентов регрессии ( 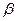- коэффициентов) в отличие от последних дают конкретную меру тесноты связи каждого фактора с результатом в числом виде. Если из стандартизованного уравнения регрессии 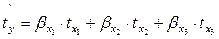следует, что 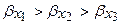т.е. по силе влияния на результат порядок факторов таков: то этот же порядок факторов определяется и по соотношению частных коэффициентов корреляции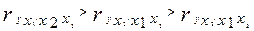

Согласованность частной корреляции и стандартизованных коэффициентов регрессии наиболее отчетливо видна из сопоставления их формул при двухфакторном анализе. Для уравнения регрессии в стандартизованном масштабе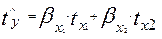

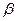- коэффициенты могут быть определены по формулам, вытекающим из решения системы уравнений:

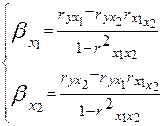(3.29)

Сравнивая их с рекуррентными формулами расчета частных коэффициентов корреляци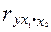и и 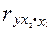можно видеть, что

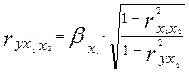
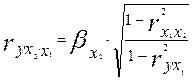(3.30)

Иными словами, в двух факторном анализе частные коэффициенты корреляции - это стандартизованные коэффициенты регрессии, умноженные на корень квадратный из соотношения долей остаточных дисперсий фиксируемого фактора на фактор и на результат.

В эконометрике частные коэффициенты корреляции обычно не имеет самостоятельного значения. В основном их используют на стадии формирования модели, в частности в процедуре отсева факторов. Так, строя многофакторную модель, например, методом исключения переменных, на первом шаге определяется уравнение регрессии с полным набором факторов и рассчитывается матрица частных коэффициентов корреляции. На втором шаге отбирается фактор с наименьшей и не существенной по т- критерию Стьюдента величиной показателя частной корреляции. Исключив его из модели, строится новое уравнение регрессии. Процедура продолжается до тек пор, пока не окажется, что все частые коэффициенты корреляции существенно отличается от нуля. Если исключен несущественный фактор, то множественны коэффициенты детерминации на двух смежных друг от друга, т.е 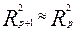где р- число факторов.

Из приведенных ранее формул частных коэффициентов корреляции видна связь этих показателей с совокупным коэффициентом корреляции. Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка ), можно определить совокупный коэффициент корреляции по формуле

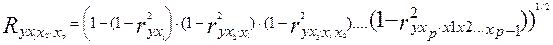
При полной зависимости результативного признака от исследуемых факторов коэффициент совокупного их влияния равен единице. Из единицы вычитается доля остаточной вариации результативного признака (1- 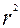), обусловленная последовательно включенными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов.

В рассмотренном примере с тремя факторами величина коэффициента множественной корреляции составила :

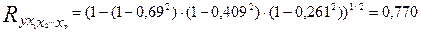
Величина множественного коэффициента корреляции всегда больше (или равна) максимального частного коэффициента корреляции, что имеет место в нашем примере: 0,770 по сравнению с 0,505