Взаимосвязь 2 форм записи уравнения касательной.
Полученное выше уравнение действительно является другой формой того уравнения касательной, которое мы выводили раньше, а именно 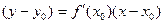 . Покажем это подробнее.
. Покажем это подробнее.
Пусть 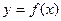 явное уравнение кривой. Можно легко свести его к неявному:
явное уравнение кривой. Можно легко свести его к неявному: 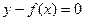 . Функция
. Функция 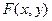 это как раз и есть
это как раз и есть 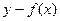 .
.
Тогда 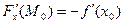 ,
, 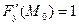 , значит, уравнение
, значит, уравнение
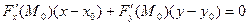
примет вид: 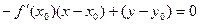 , то есть
, то есть 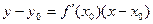 .
.
Также можно и наоборот, в уравнении 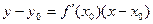 записать производную по формуле
записать производную по формуле 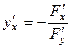 . Тогда
. Тогда 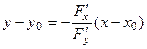
из чего следует 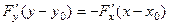 , что и приводит к уравнению
, что и приводит к уравнению
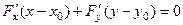 .
.
Выведем уравнение касательной плоскости к поверхности.
Теперь, когда нам известен вектор нормали к поверхности, а именно, что 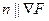 (градиент расположен именно по нормали), можно воспользоваться тем методом, который применяли в геометрии для вывода уравнения плоскости по точке и нормали. Точка
(градиент расположен именно по нормали), можно воспользоваться тем методом, который применяли в геометрии для вывода уравнения плоскости по точке и нормали. Точка 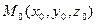 , нормаль
, нормаль 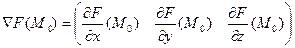 .
.
Это можно записать, используя более короткие обозначения: 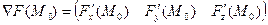 .
.
Если взять произвольную точку 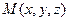 в касательной плоскости, то вектор
в касательной плоскости, то вектор 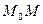 ортогонален
ортогонален 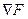 .
.
Тогда скалярное произведение векторов 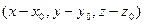 и
и 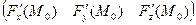 равно 0.
равно 0.
Итак, уравнение касательной плоскости:
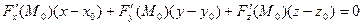 .
.
Формула Тейлора.
Согласно уравнению касательной, ординату точки на касательной можно записать так: 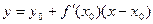 , то есть
, то есть 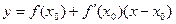 . Как можно сразу заметить, в точке
. Как можно сразу заметить, в точке 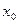 она совпадает со значением функции, то есть
она совпадает со значением функции, то есть 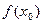 . Чем дальше удаляемся от точки
. Чем дальше удаляемся от точки 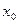 , тем разнность между ординатой точки на касательной и точки на графике становится больше. Обозначим эту разность через
, тем разнность между ординатой точки на касательной и точки на графике становится больше. Обозначим эту разность через 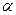 :
:
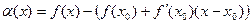 . Так как она стремится к 0 при
. Так как она стремится к 0 при 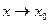 , то можно сказать, что
, то можно сказать, что 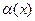 является бесконечно малой в
является бесконечно малой в 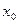 . Вот эта разность между f и касательной показана жёлтым цветом:
. Вот эта разность между f и касательной показана жёлтым цветом:

Если изобразить график 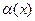 то он похож на параболу. Как сейчас увидим, это не случайно, там действительно появится 2-я степень. Если выделить главную часть этой бесконейно малой
то он похож на параболу. Как сейчас увидим, это не случайно, там действительно появится 2-я степень. Если выделить главную часть этой бесконейно малой 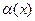 , то она будет, по крайней мере, не 1-го порядка, а более высокого, потому что первая степень полностью учтена в том слагаемом, которое из уравнения касательной. Тейлор доказал, что её главная часть зависит от второй производной, и равна
, то она будет, по крайней мере, не 1-го порядка, а более высокого, потому что первая степень полностью учтена в том слагаемом, которое из уравнения касательной. Тейлор доказал, что её главная часть зависит от второй производной, и равна 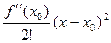 . Касательная даёт очень грубое приближённое значение функции, а с учётом этого слагаемого, получится что мы задаём уже не многочленом 1-й степени, а 2-й степени, то есть более точное приближение, чем это было для касательной.
. Касательная даёт очень грубое приближённое значение функции, а с учётом этого слагаемого, получится что мы задаём уже не многочленом 1-й степени, а 2-й степени, то есть более точное приближение, чем это было для касательной.
Если теперь и это слагаемое отнять от f(x), то получится
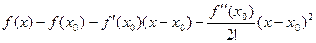 но это снова бесконечно-малая, из неё снова можно выделить главную часть, которая уже будет 3 порядка. Тогда получится многочлен 3 степени, который ещё точнее задаёт функцию
но это снова бесконечно-малая, из неё снова можно выделить главную часть, которая уже будет 3 порядка. Тогда получится многочлен 3 степени, который ещё точнее задаёт функцию 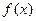 . Если этот процесс продолжить до бесконечности, то получится формула:
. Если этот процесс продолжить до бесконечности, то получится формула:
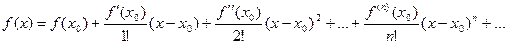
А если остановить на n-м шаге, то f будет задана приближённо с помощью многочлена n-й степени.
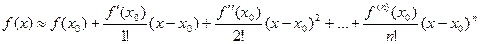
Погрешность в этом случае можно записать в виде 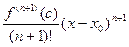 , где
, где 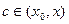 .
.
Если начальная точка, в окрестности которой ищется разложение на степенные функции, это 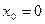 , то
, то
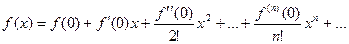 называется формулой Маклорена.
называется формулой Маклорена.
Полный вывод формулы Тейлора проводится в курсе комплексного анализа (ТФКП) так как основан на свойствах комплексных функций. Однако мы сейчас можем рассмотреть другую краткую идею доказательства. Продифференцируем равенство
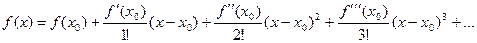
получим
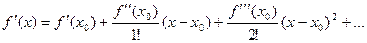
Если при этом обозначить первую производную: 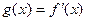 то мы бы получили такую запись:
то мы бы получили такую запись:
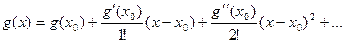 то есть, точно такая же формула Тейлора верна и для производной. Если теперь допустить, что коэффициенты в формуле Тейлора как-либо отличались бы от
то есть, точно такая же формула Тейлора верна и для производной. Если теперь допустить, что коэффициенты в формуле Тейлора как-либо отличались бы от 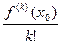 , то при дифференцировании бы не сократился последний множитель из факториала, то есть для производной формула была бы уже не верна. То есть, тогда она была бы не верна в классе непрерывных функций, потому что для каждой функции
, то при дифференцировании бы не сократился последний множитель из факториала, то есть для производной формула была бы уже не верна. То есть, тогда она была бы не верна в классе непрерывных функций, потому что для каждой функции 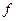 сразу нашлась бы такая функция
сразу нашлась бы такая функция 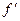 , для которой эта формула была бы не верна.
, для которой эта формула была бы не верна.
Уравнение касательной - это самая короткая из формул Тейлора, это самое грубое приближение, где учтена только 1-я степень.
Примеры рядов Тейлора некоторых известных функций.
Пример. 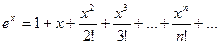
Выведем эту формулу. Рассмотрим несколько производных и затем их значения в точке 0:
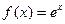
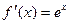
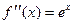 ...
...
| 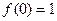
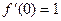
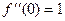 ...
...
|
тогда мы и получаем, что: 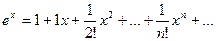 т.е
т.е 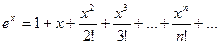 .
.
Вот как выглядят графики многочленов и экспоненты:
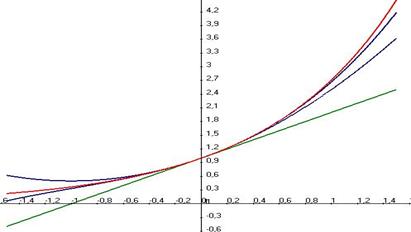
Красным показан график экспоненты, зелёным - касательная, затем 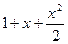 и
и 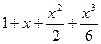 .
.
Как видно, уже даже для 3 степени погрешность очень мала.
Пример. 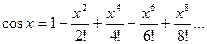
Выведем эту формулу. Рассмотрим несколько производных и затем их значения в точке 0:
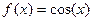
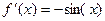
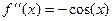
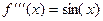 ...
...
| 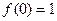
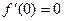
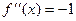
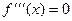 ...
...
|
Далее 4 производная совпадает с 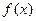 и повторение через каждые 4 шага. Подставим эти константы в формулу:
и повторение через каждые 4 шага. Подставим эти константы в формулу:
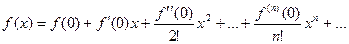 и получим
и получим 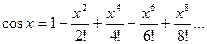 А вот как это всё выглядит на графике:
А вот как это всё выглядит на графике:
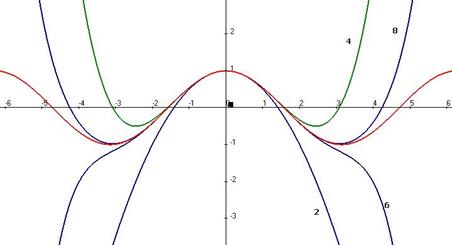
Красным цветом показан график 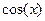 .
.
Цифрой 2 помечен график функции 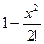 (в которой включены до второй степени включительно), цифрой 4 - график
(в которой включены до второй степени включительно), цифрой 4 - график 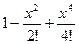 , далее, кривая, помеченная «6» соответствует
, далее, кривая, помеченная «6» соответствует 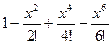 , а «8» это
, а «8» это 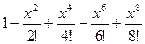 . Как видим, чем больше степень, тем на большем промежутке наблюдается почти полное совпадение многочлена с косинусом. Если взять степени до 8-й, то совпадение происходит почти весь период от
. Как видим, чем больше степень, тем на большем промежутке наблюдается почти полное совпадение многочлена с косинусом. Если взять степени до 8-й, то совпадение происходит почти весь период от 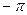 до
до 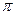 .
.
Формула Тейлора для синуса выводится аналогичным образом.
(подробнее эту и другие функции рассмотрим на практике).
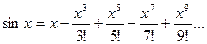
Дата добавления: 2016-12-26; просмотров: 1163;
