Теорема 2. (Ферма) (необходимый признак экстремума).
Если функция дифференцируема в точке 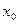 , и
, и 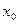 - точка экстремума, то
- точка экстремума, то 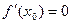 .
.
Доказательство опирается на теорему 1. Если допустить, что точка экстремума, но производная не 0, то тогда производная в точке равна какому-то числу, положительному или отрицательному. А тогда по прошлой теореме, справа и слева от этой точки график то выше, то ниже, то есть 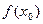 не может быть экстремальным значением во всей окрестности.
не может быть экстремальным значением во всей окрестности.
Замечание.Если функция дифференцируема, а следовательно и непрерывна, то 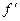 должна при возрастании из отрицательных значений в положительные пройти через 0. Если же разрывна, то можете перескочить через 0, так чтобы 0 не был знаением ни в одной точке. Поэтому эта теорема и не применима для функции
должна при возрастании из отрицательных значений в положительные пройти через 0. Если же разрывна, то можете перескочить через 0, так чтобы 0 не был знаением ни в одной точке. Поэтому эта теорема и не применима для функции 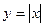 . Для неё производная равна
. Для неё производная равна 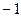 до начала координат, а потом сразу 1, проходит через разрыв 1 рода, то есть скачок, и производная в точке минимума не равна 0, а сразу перескочила в положительное значение.
до начала координат, а потом сразу 1, проходит через разрыв 1 рода, то есть скачок, и производная в точке минимума не равна 0, а сразу перескочила в положительное значение.
Теорема 3. (достаточный признак экстремума на основе 1-й производной)
1). Если 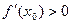 при
при 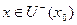 и
и 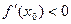 при
при 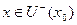 то
то 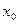 - точка максимума,
- точка максимума,
2). Если 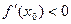 при
при 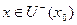 и
и 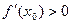 при
при 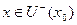 то
то 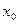 - точка минимума.
- точка минимума.
Доказательство.
Если до точки 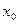 производная больше нуля, то это значит, что функция возрастает в левой полуокрестности. При возрастании, чем правее точка, тем больше в ней значение. Но ведь
производная больше нуля, то это значит, что функция возрастает в левой полуокрестности. При возрастании, чем правее точка, тем больше в ней значение. Но ведь 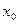 это правая граница множества
это правая граница множества 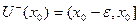 . Таким образом,
. Таким образом, 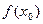 наибольшее значение во множестве
наибольшее значение во множестве 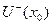 .
.
При убывании, чем правее точка, тем меньше в ней значение. Но ведь 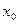 это левая граница множества
это левая граница множества 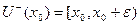 . Таким образом,
. Таким образом, 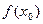 наибольшее значение также и во множестве
наибольшее значение также и во множестве 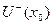 . Получается, что
. Получается, что 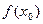 - наибольшее значение во всём множестве
- наибольшее значение во всём множестве 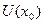 , а это и есть максимум.
, а это и есть максимум.
Доказали подробно 1-й пункт, 2-й аналогичными рассуждениями с заменой неравенств на противоположные.
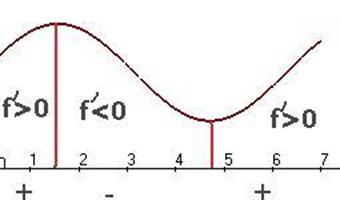
Итак, на стыке интервалов монотонного роста и убывания - точки экстремума. Таким способом и можно находить экстремумы. Кстати, для теоремы 3 всё равно, гладкая функция или точка излома (производная разрывна) в точке экстремума. Она применима и для функции 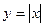 .
.
Теперь становится ясно, почему у кубической параболы нет экстремума в точке (0,0): интервал роста сменяется снова на интервал роста, поэтому, хоть даже и производная равна 0, но экстремума там нет.
Пример. Найти экстремумы 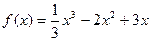 .
.
Решение. Найдём 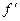 =
= 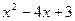 . Корни 1 и 3. Выясним знак производной на каждом из интервалов
. Корни 1 и 3. Выясним знак производной на каждом из интервалов 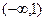 ,
, 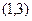 и
и 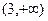 . Для этого надо вычислить знак
. Для этого надо вычислить знак 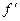 в какой-нибудь точке на каждом из этих интервалов. Желательно для удобства вычислений взять целое число как представителя интервала.
в какой-нибудь точке на каждом из этих интервалов. Желательно для удобства вычислений взять целое число как представителя интервала.
Например, 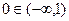 ,
, 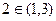 и
и 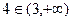 .
.
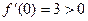 .
. 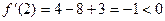 .
. 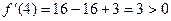 .
.
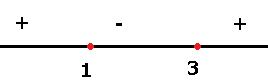
Таким образом, в точке 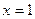 рост сменяется убыванием,
рост сменяется убыванием, 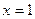 точка максимума. В точке
точка максимума. В точке 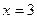 убыванием сменяется ростом,
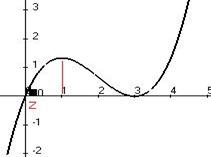
убыванием сменяется ростом, 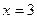 точка минимума. Можно вычислить и ординаты, чтобы более подробно нарисовать график. Точки экстремума (1, 4/3) и (3, 0) . Вот график:
точка минимума. Можно вычислить и ординаты, чтобы более подробно нарисовать график. Точки экстремума (1, 4/3) и (3, 0) . Вот график:
Теорема 4. (достаточный признак экстремума на основе 2-й производной)
Если функция дважды дифференцируема, и 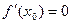 , то:
, то:
при 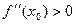 - то в точке
- то в точке 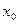 минимум,
минимум,
при 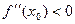 в точке
в точке 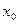 максимум.
максимум.
Доказательство.
Если вторая производная больше нуля, значит, первая производная возрастает при прохождении через точку 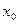 . То есть, до точки
. То есть, до точки 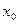 она была отрицательна, а после положительна. Т.е.
она была отрицательна, а после положительна. Т.е. 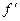 переходит из - в + , то есть точка на стыке интервалов убывания и роста. По теореме 3 это и означает, что там минимум. Изобразим семейство касательных в точках вокруг минимума:
переходит из - в + , то есть точка на стыке интервалов убывания и роста. По теореме 3 это и означает, что там минимум. Изобразим семейство касательных в точках вокруг минимума:

касательная была направлена вниз, а после прохождения через эту точку - повернётся вверх.
Аналогично, если 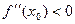 , то
, то 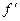 убывающая, что означает, что она проходит через 0 именно в процессе убывания, т.е. положительная в левой полуокрестности и отрицательна в правой. По теореме 3 это и означает, что в точке
убывающая, что означает, что она проходит через 0 именно в процессе убывания, т.е. положительная в левой полуокрестности и отрицательна в правой. По теореме 3 это и означает, что в точке 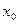 максимум. Теорема доказана.
максимум. Теорема доказана.
Замечание. Этот факт легко запомнить: для параболы 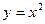 вторая производная равна +2, а там минимум, так как ветви этой параболы направлены вверх. Для
вторая производная равна +2, а там минимум, так как ветви этой параболы направлены вверх. Для 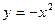 будет
будет 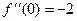 , для неё - максимум.
, для неё - максимум.
Решим тот же самый пример теперь с помощью 2 производной. 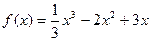 ,
, 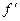 =
= 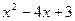 . Точки с нулевой производной 1 и 3. А теперь не будем искать знак производной на каждом интервале, а просто вычислим
. Точки с нулевой производной 1 и 3. А теперь не будем искать знак производной на каждом интервале, а просто вычислим 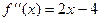 .
.
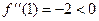 в точке
в точке 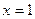 максимум.
максимум.
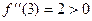 в точке
в точке 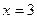 минимум.
минимум.
Но что делать, если окажется 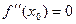 ? Как видим, такие ситуации тоже бывают, например, рассмотрим функции
? Как видим, такие ситуации тоже бывают, например, рассмотрим функции 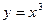 и
и 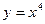 . Для
. Для 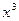 ,
, 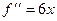 ,
, 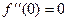 и там нет экстремума. Для 4-й степени,
и там нет экстремума. Для 4-й степени, 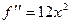 , тоже
, тоже 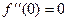 , но для
, но для 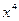 есть минимум в нуле. В чём же разница и как узнавать, есть ли экстремум? На этот вопрос отвечает следующая теорема.
есть минимум в нуле. В чём же разница и как узнавать, есть ли экстремум? На этот вопрос отвечает следующая теорема.
Дата добавления: 2016-12-26; просмотров: 1331;
