Основные теоремы дифф. исчисления
Теорема Ролля.Если функция f непрерывна и дифференцируема на [a,b], и 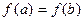 , то существует точка
, то существует точка 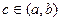 , такая что
, такая что 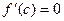 .
.
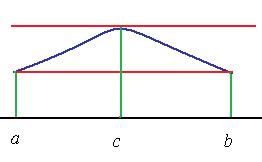
Доказательство. Если в точке 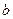 такое же значение, как было в точке
такое же значение, как было в точке 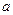 , то:
, то:
1) либо функция тождественно равна константе (но тогда вообще в любой точке нулевая производная)
2) либо не константа, но тогда она должна достигать какого-то максимального отклонения от ординаты 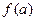 и снова возвращаться на эту же высоту, в этом случае есть точка экстремума, одна или несколько. Из теоремы Ферма об эстремуме следует, что в такой точке производная равна 0.
и снова возвращаться на эту же высоту, в этом случае есть точка экстремума, одна или несколько. Из теоремы Ферма об эстремуме следует, что в такой точке производная равна 0.
Теорема Лагранжа.Если функция f непрерывна и дифференцируема на [a,b], то существует точка 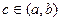 , такая что
, такая что 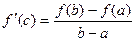 .
.
Пояснение. Теорема Лагранжа фактически утверждает, что на графике есть такая точка, что касательная в ней наклонена под таким же углом, как хорда, соединяющая 2 конца графика в точках 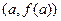 и
и 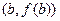 . Чертёж:
. Чертёж:
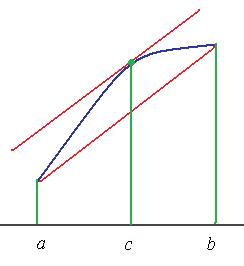
Доказательство. Рассмотрим функцию 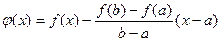 .
.
Вычислим, чему она равна в точках 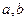 .
.
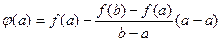 =
= 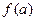
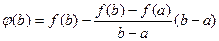 =
= 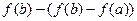 =
= 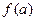 .
.
Итак, на концах интервала значение одно и то же. Тогда по теореме Ролля существует точка 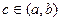 , где
, где 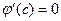 . Рассмотрим подробнее производную
. Рассмотрим подробнее производную 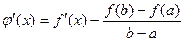 . Дробь здесь фактически просто коэффициент k, он не содержим переменную, дифференцируется только
. Дробь здесь фактически просто коэффициент k, он не содержим переменную, дифференцируется только 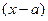 .
.
В точке с: 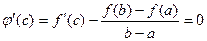 , тогда
, тогда 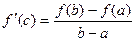 .
.
Теорема Коши.Если функции f,g непрерывны и дифференцируемы на [a,b], то существует точка 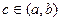 , такая что
, такая что 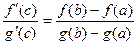 .
.
Доказательство. Рассмотрим 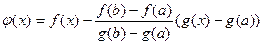 .
.
Проверим её значения на концах интервала, они одинаковы:
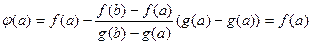 .
.
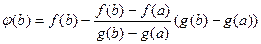 =
= 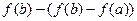 =
= 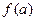 .
.
Тогда по теореме Ролля существует точка 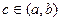 , где
, где 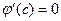 .
.
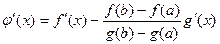 , тогда
, тогда 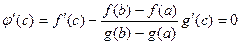 ,
,
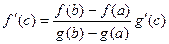 , в итоге
, в итоге 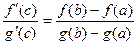 .
.
Теорема Лопиталя.Функции f,g непрерывны и дифференцируемы на [a,b], и 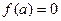 ,
, 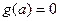 . Тогда
. Тогда 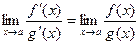 .
.
Доказательство. Если применить теорему Коши к отрезку [a,x].
В некоторой точке 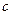 верно:
верно: 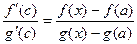 =
= 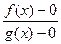 .
.
Но при 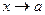 , точка с, лежащая между a,x тоже стремится к а.
, точка с, лежащая между a,x тоже стремится к а.
Тогда 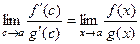 .
.
Дата добавления: 2016-12-26; просмотров: 638;
