Выпуклость вверх (вниз) графика функции и 2 производная.

Выпуклое множество.

Определение. Множество D называется выпуклым, если для любой пары точек этого множества отрезок, соединяющий их, состоит из точек, принадлежащих этому множеству.

В первом примере множество выпуклое, во втором нет: есть пары точек, такие, что кратчайшая линия, соединяющая их, выходит за пределы этого множества.

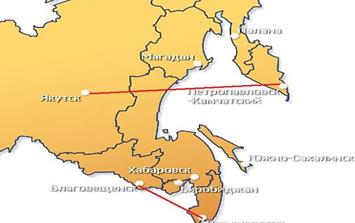
Ещё пример не выпуклого множества на карте. Если лететь с Каматки, то кратчайшая линия проходит над морем, а если из Владивостока - над чужой территорией. Есть соединяющая линия, проходящая по своей территории и именно над сушей, но она - не кратчайшая.

Для графиков функций эти понятия обобщаются так.

Функция называется выпуклой вверх (соотв., вниз) на отрезке [a,b], если график проходит выше (соотв., ниже) любой хорды, соединяющей пару точек на графике.

На чертеже: для выпуклой вверх функции , для выпуклой вниз .

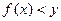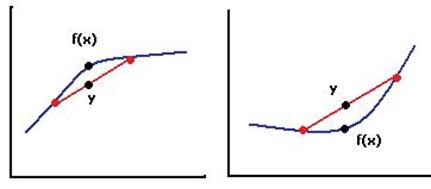
В случае, когда f выпукла вверх, множество точек, расположенных под графиком является выпуклым множеством, а если выпуклая вниз - то выпуклое множество точек, лежащих над графиком.

Если f выпукла вверх, то угол наклона касательной уменьшается при движении точки вправо, то есть 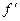убывает, а это происходит тогда и только тогда, когда .

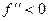Если f выпукла вниз, то соответственно 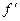возрастает, а .

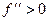Теорема. Функция выпукла вверх 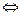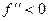, функция выпукла вниз .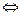

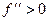Определение. Если 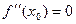, при этом в правой и левой полуокрестности 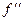разного знака, то точка 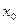называется точкой перегиба.

Точки перегиба хорошо видны и в реальной жизни: если дорога поворачивает сначала в одну сторону, например влево (при этом линия дороги выпукла вправо) а потом дорога закругляется вправо (линия при этом выпукла влево), то между ними точка перегиба.

Если мы проезжаем кольцо, то траектория движения сначала выпукла влево (заезжаем на кольцо), потом вправо (движемся по кольцу), потом снова влево (когда съезжаем с кольца на следующую часть дороги).

Пример 1. Найти интервалы выпуклости и точки перегиба для .

, , .

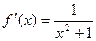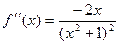При 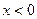: 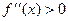, f выпукла вниз.

При 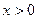: 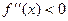, f выпукла вверх.

Касательная сначала поворачивается вверх, 1-я производная растёт (в начале координат угол наклона доходит до 45 градусов), а потом снова опускается при удалении точки в .

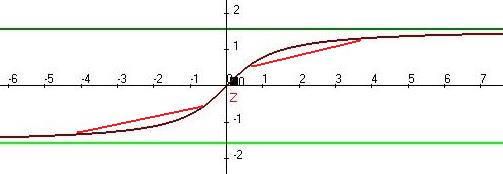
Пример 2. Найти интервалы выпуклости и точки перегиба для функции .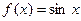

Вторая производная: .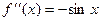

На 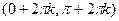: 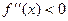, f выпукла вверх.

На : 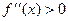, f выпукла вверх.

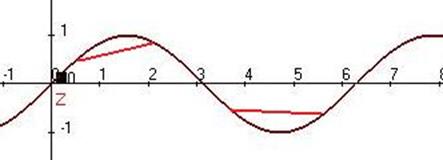
Точки перегиба: .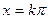

Асимптоты.

Если при удалении точки графика в бесконечность, она сближается с некоторой прямой, то эта прямая называется асимптотой.

Так как удаление от начала координат в бесконечность может происходить как вправо/влево, так и вверх/вниз либо вообще по диагонали, то можно эту ситуацию описать одним общим условием:
Если 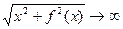то .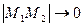

Горизонтальные асимптоты:

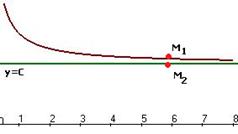
Если , , то асимптота горизонтальная, эта ситуация имеет место, когда .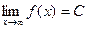

Вертикальные асимптоты:

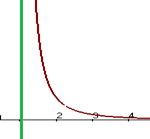
Если 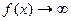, , 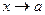то асимптота вертикальная (это соответствует разрыву 2 рода, ).

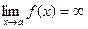Наклонные асимптоты:

Если 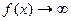, , но при этом график всё же стремится к некоторой прямой, то асимптота наклонная.

Как видно, что во всех этих случаях точка неограниченно удаляется в бесконечность, но 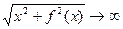за счёт либо 1-го слагаемого, либо 2-го, либо двух сразу.

Наклонные асимптоты. Вывод формул и .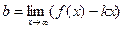

Так как точка на графике и на асимптоте сближаются то:

.

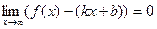Отсюда следует, что 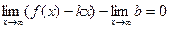, то есть

.

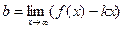Рассмотрим прямую 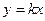, параллельную асимптоте .

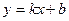Если разность ординат для точки на графике и соответствующей точки на прямой 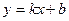стремится к 0, то разность ординат для точки на графике и точки на прямой 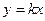стремится к 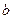. Отрезок, соответствующий этому расстоянию, отмечен красным на чертеже.

Если две величины, и 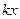, неограниченно возрастают, и при этом разность между ними не увеличивается, а стремится к константе, то их отношение стремится к 1, то есть 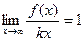. Но тогда .

Итак, мы получили формулы для нахождения 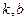. На практике сначала надо найти 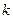, а уже затем .

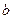Пример. Найти асимптоты графика функции .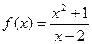

Решение. Во-первых, сразу видно точку разрыва 2-го рода 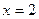. Есть вертикальная асимптота .

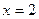Найдём наклонную асимптоту.

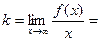
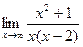(мы просто добавили лишний 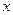в знаменателе, тем самым поделили на ).

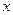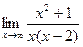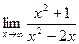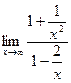= = = 1. Итак, .

Обратите внимание: здесь предел одинаково вычисляется при и при 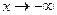, но бывают примеры, в которых по-разному, то есть на правой и левой полуплоскости могут быть разные асимптоты.

Найдём 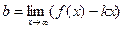= = 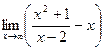= = 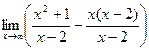= = 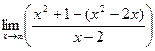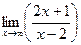2.

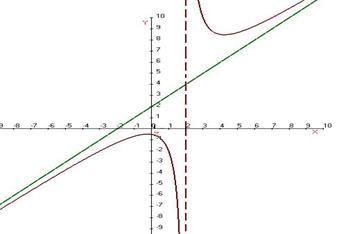
Ответ. Вертикальная x = 2, наклонная y = x + 2.

График выглядит так:

Замечание. При значении 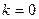ситуация не однозначна: не всегда существует горизонтальная асимптота, например, для ln(x) горизонтальной асимптоты нет, несмотря на то, что 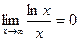. Коэффициент 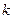лишь выявляет, к чему стремится угловой коэффициент касательной. Но для ln(x) касательная стремится к горизонтальному положению, тем не менее, функция не ограничена сверху.

Замечание. Если на данной полуплоскости, правой или левой, есть наклонная асимптота, то нет горизонтальной, и наоборот, если есть горизонтальная, то нет наклонной. Действительно, ситуации 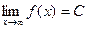(что требуется для горизонтальной асимптоты) и 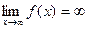(при существовании наклонной, f возрастает к 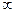) взаимоисключающие.

Замечание.Если получается , тогда нет наклонной асимтоты. Например, при 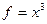, деление на 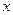ни к чему не приведёт, всё равно останется . .

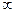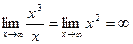Лекция № 16. 23. 12. 2016