Экстремум функции нескольких переменных.

Определение (запишем для 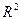, но аналогично и для n-мерного).

Пусть 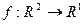, то есть 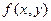. Точка 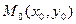называется точкой максимума (минимума), если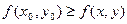 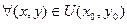(для минимума соответственно, ).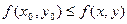

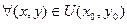Идея здесь та же самая, что и для функций одной переменной: максимум, если значение функции больше, чем в любой точки из окрестности, а минимум, если меньше. просто окрестность в плоскости это не интервал, а круг. А в пространстве - шар.

Физический смысл экстремума функции n переменных. Если задано распределение температур в пространстве, то есть точка максмальной и минимальной температуры. Так, существует точка минимальной температуры в земной атмосфере.

Пример. .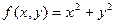

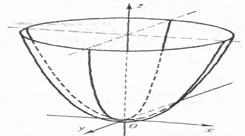
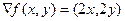. Вертикальные сечения параболоида - это параболы, ветвями направленные вверх, для них как для кривых просто обычный минимум. В точке (0,0) частные производные нулевые, т.е. 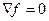в точке (0,0).

Аналог необходимого признака, т.е. теоремы Ферма, здесь имеет место: Если 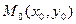точка экстремума, то .

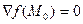Аналог достаточного признака на основе 2-й производной здесь выглядит более сложно, но тоже имеет место. Если вычислить все возможные вторые производные, то они образуют матрицу:

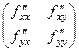
в данном случае она равна 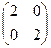, соответствует положительно-определённой квадратичной форме 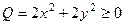. В каждом из двух перпендикулярных сечений поверхности такая кривая, что 2-я производная больше нуля, то есть по каждому сечению минимум. При этом все угловые миноры больше нуля. Для данной матрицы это очевидно, однако если бы она была не диагональная, то именно проверка знаков угловых миноров позволяла бы точно сказать, есть ли в точке экстремум.

Для сравнения, рассмотрим функцию 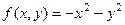. Для неё точка (0,0) является точкой максимума. .

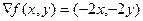Посмотрим, как при этом устроена матрица вторых производных.

= .

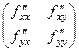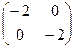Для каждого отдельно взятого сечения вдоль оси 0x или оси 0y, как для обычной кривой, есть максимум, вторая производная равна 0. Если же исследовать знаки угловых миноров, то они чередуются, начиная с отрицательного. Это достаточное условие максимума для функции n переменных. Если матрица диагональная, то это означает, что на диагонали все элементы отрицательны.

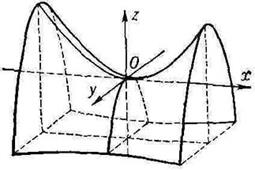
Если градиент равен 0-вектору, это вовсе не является достаточным условием экстремума. Так, есть функции, для которых градиент 0, а экстремума нет, так как в одном сечении минимум, а в другом сечении максимум. Гиперболический параболоид:

, , .

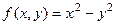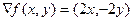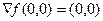Однако матрица вторых производных такая:

= .

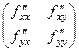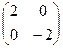Не выполняется ни одно из свойств: угловые миноры не положительны, но и их знаки не чередуются, начиная с минуса. Видно, что для параболы в сечении в плоскости 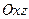минимум, а в перпендикулярном сечении в плоскости 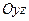максимум.