Условный экстремум.

Рассмотрим эллиптический параболоид, сделаем сечение вертикальной плоскостью, которая параллельна координатной плоскости. Для самой поверхности точка М ничем не характерна, рядом с ней есть и точки меньшей, и точки большей высоты. Но вот для сечения это - минимум.

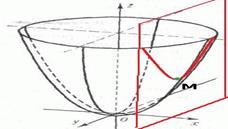
То есть, если сузить область определения с плоской фигуры до одномерной линии, то от поверхности останется сечение, и для сечение, уже как просто для кривой, могут быть экстремумы, которых не было на самой поверхности. такие экстремумы называются «условными», потому что для сужения области определения применяется какое-то условие. Неявно задать кривую можно с помощью какого-то условия типа 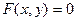. Например, показанное на чертеже сечение получается, если фиксировать x, т.е. здесь условие вида 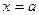, то есть 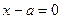. Итак, определение.

Определение. Пусть задана функция 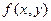и некоторое неявное уравнение кривой 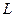в плоскости 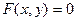. Точка 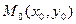называется точкой условного максимума, если 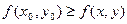для любой точки 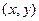принадлежащей .

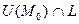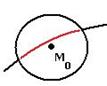
Отличие от обычного максимума: для максимума в центре окрестности должно быть значение больше, чем в любой точке окрестности, а для условного максимума больше, чем во всех точках пересечения этой окрестности и кривой 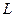. (В других точках из окрестности, которые не принадлежат кривой, может быть не больше, а меньше).

Определение условного минимума вводится аналогично, лишь в неравенстве изменён знак: .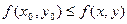

Эти понятия нужны для того, чтобы искать наибольшие и наименьшие значения в плоских областях. Ведь граница плоской области это линия, а не две точки a,b как было при поиске наибольшего значения на отрезке.

На наклонной плоскости, то есть для поверхностей типа 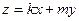, вообще нет точек экстремума, т.к. рядом с любой точкой есть другие точки, как выше, так и ниже. Градиент этой функции равен 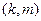и он, очевидно, не равен (0,0). Но если сузить область определения, провести параболу под этой наклонной плоскостью, то на плоскости будет кривая, у которой уже есть точка минимальной высоты!

Пример. Дана функция 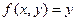. Найти условный экстремум этой функции на параболе .

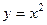Решение. Условие имеет вид .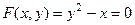

Выразим все имеющиеся в функции 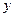через .

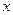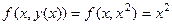. Обычная производная 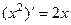, минимум в точке 0. Тогда 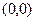условный минимум. Чертёж:

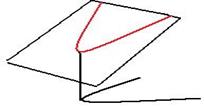
Пример.Найти отношение сторон прямоугольника, такое, что при фиксированном периметре получилась бы максимальная площадь.

Решение.Периметр 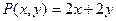. Площадь выражается функцией 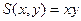. Если периметр фиксирован, например приравняем к константе 2С, то 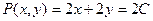, это условие позволит нам одну переменную выразить через другую. 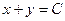, т.е. 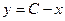. Подставим в функцию 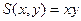, получим 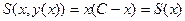. Функция стала зависеть только от одной переменной, и для неё уже можно искать экстремумы обычным способом. 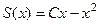, тогда .

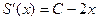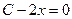
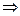
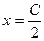. Это именно максимум т.к. .

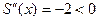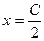
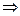
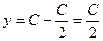. Тогда отношение .

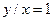Ответ. 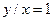. То есть, среди прямоугольников равного периметра, наибольшей площадью обладает квадрат.

Замечание. Представим, что квадрат размера 1 на 1, периметр равен 4. Так вот, при увеличении одной стороны до 2 вторая уменьшается до 0 и соответственно, площадь до 0. Для прямоугольника со сторонами 2 и 0 периметр формально тоже равен 4.