Экстремумы и строение графика.
Монотонность и знак производной.
Вспомним определение монотонного роста и убывания: если при 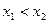 выполняется
выполняется  , то функция монотонно возрастает, а если
, то функция монотонно возрастает, а если  то монотонно убывает. Рассмотрим, как монотонность взаимосвязана со знаком 1-й производной.
то монотонно убывает. Рассмотрим, как монотонность взаимосвязана со знаком 1-й производной.
Лемма. 1)  тогда и только тогда, когда
тогда и только тогда, когда 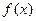 монотонно возрастает.
монотонно возрастает.
2) 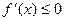 тогда и только тогда, когда
тогда и только тогда, когда 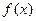 монотонно убывает.
монотонно убывает.
Доказательство. Рассмотрим функцию 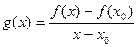 (это та самая функция, которая была в определении предела).
(это та самая функция, которая была в определении предела).
Предел 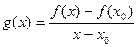 при
при 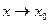 это и есть
это и есть 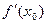 .
.
Возьмём 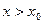 . Если f мнонтонно возрастает, то при этом
. Если f мнонтонно возрастает, то при этом 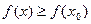 , то есть дробь положительна. Если функция
, то есть дробь положительна. Если функция 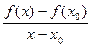 положительна, то и её предел больше нуля, тогда
положительна, то и её предел больше нуля, тогда  .
.
Аналогично, если функция 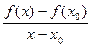 отрицательна, то и её предел меньше нуля, тогда
отрицательна, то и её предел меньше нуля, тогда 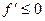 .
.
Определение 1(точки наибольшего, наименьшего значения в D).
Пусть функция f - функция одной переменной, т.е. отображает некоторое множество 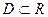 в
в 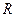 . Точка
. Точка 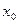 называется точкой наибольшего (соответственно, наименьшего) значения в D, если
называется точкой наибольшего (соответственно, наименьшего) значения в D, если 
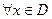 . (соответственно,
. (соответственно, 
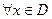 ).
).
Примечание. Здесь 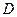 это область определения, может совпадать со всей числовой прямой, но не обязательно.
это область определения, может совпадать со всей числовой прямой, но не обязательно.
Определение 2. (максимум и минимум)
Пусть функция 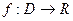 . Точка
. Точка 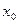 называется точкой максимума (минимума), если существует окрестность
называется точкой максимума (минимума), если существует окрестность 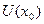 точки
точки 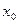 , такая, что
, такая, что 
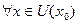 . (для минимума
. (для минимума 
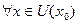 ).
).
Для максимума и минимума есть общее название - «экстремум».
Локальных максимумов в смысле определения 2 может быть несколько или даже бесконечное количество. Например, график 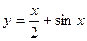 , здесь через каждые
, здесь через каждые 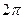 есть новый максимум, который выше того, что слева от него:
есть новый максимум, который выше того, что слева от него:
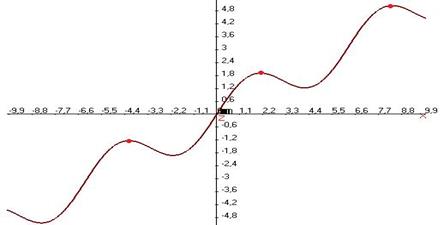
Понятие «максимум» отличается от понятия «наибольшее значение» тем, что для максимума требуется, чтобы функция была наибольшей в некоторой окрестности, а для наибольшего значения - во всей области.
Взаимосвязь между равенством нулю первой производной и экстремумом не однозначна. Так, функция 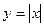 имеет минимум в точке 0, но там не существует производная, то есть нельзя сказать, что
имеет минимум в точке 0, но там не существует производная, то есть нельзя сказать, что 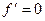 . А для функции
. А для функции  ,
, 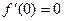 , но при этом нет экстремума.
, но при этом нет экстремума.
Рассмотрим подробно структуру функции в случае, когда производная не равна 0.
Теорема 1.
1). Если 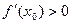 то:
то:
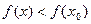 при
при 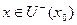 и
и 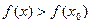 при
при  .
.
2). Если 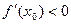 то:
то:
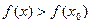 при
при 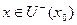 и
и 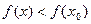 при
при  .
.
Доказательство. Рассмотрим дробь 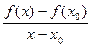 . Предел этой дроби при
. Предел этой дроби при 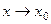 равен
равен 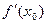 .
.
Если 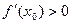 , то есть предел функции
, то есть предел функции 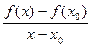 больше нуля, то в некоторой окрестности эта функция положительна. Для точки из правой полуокрестности,
больше нуля, то в некоторой окрестности эта функция положительна. Для точки из правой полуокрестности,  , верно
, верно 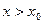 , то есть
, то есть  .
.
Но так как дробь больше нуля, 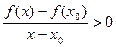 , тогда и числитель должен быть больше нуля.
, тогда и числитель должен быть больше нуля. 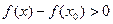 , тогда
, тогда 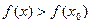 .
.
Если точка 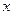 - в левой полуокрестности
- в левой полуокрестности 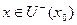 , тогда
, тогда 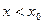 , то есть
, то есть 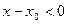 , и в положительной дроби
, и в положительной дроби  будет отрицательный знаменатель, тогда и числитель должен быть меньше нуля.
будет отрицательный знаменатель, тогда и числитель должен быть меньше нуля. 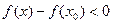 , тогда
, тогда 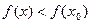 для точек
для точек 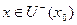 .
.
Итак, справа от точки 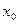 график функции выше, чем ордината
график функции выше, чем ордината 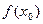 , а слева - ниже. То есть, экстремума там точно нет.
, а слева - ниже. То есть, экстремума там точно нет.
Если 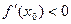 то доказывается аналогично:
то доказывается аналогично: 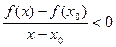 в некоторой окрестности, то при
в некоторой окрестности, то при 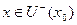 то есть положительном знаменателе, должен быть отрицательный числитель, и тогда
то есть положительном знаменателе, должен быть отрицательный числитель, и тогда 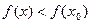 . А при
. А при 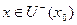 знаменатель отрицательный, тогда числитель положительный, и
знаменатель отрицательный, тогда числитель положительный, и 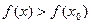 .
.
Итак, теорема доказана.
Из Т.1 следует, что если производная в точке не равна 0, а является положительным или отрицательным числом, то экстремума точно нет.
По законам логики, если из А следует В, то из отрицания В следует отрицание А. Тогда можно вывести такой односторонний факт: если экстремум есть, то производная равна 0. Правда, только с оговоркой, что производная в той точке существует. Ведь как мы видели, для модуля производная может не существовать в точке 0.
Дата добавления: 2016-12-26; просмотров: 1221;
