Теорема 5. (достаточный признак экстремума на основе старших производных).

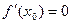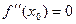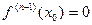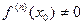Если функция n раз дифференцируема, при этом , , ..., , и . Тогда:

если n нечётно то эrстремума нет,

если n чётно, то: при 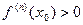- то в точке 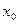минимум,

при 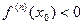в точке 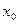максимум.

(т.е. если чётно, то аналогично 2-й производной).

Доказательство.

Запишем формулу Тейлора, причём перенесём 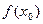влево.

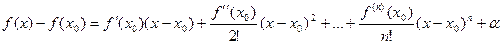Но ведь здесь первые слагаемые обнуляются по условию теоремы.

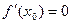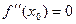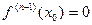, , ..., , тогда начинается именно с n-го слагаемого. 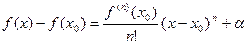, где 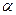- бесконечно малая более высокого порядка, чем n, то есть в некоторой окрестности она по модулю меньше чем 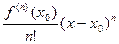и её знак уже не влияет на знак всего выражения. Тогда фактически, тогда знак разности 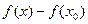в окрестности точки 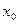зависит от знака выражения .

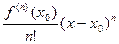При чётном n множитель 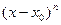всегда неотрицателен

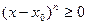
n! по построению положительное число .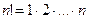

Значит, при 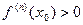получится всё выражение 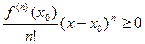, тогда 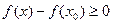в окрестности точки 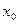, то есть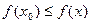 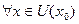. Это значит, что в точке 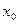минимум.

А если 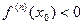, то 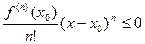, и тогда 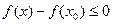а значит,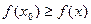 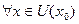. Это значит, что в точке 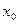максимум.

Если n нечётно, то 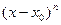разного знака в правой и в левой полуокрестности, то есть какого бы знака ни было число 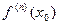, выражение 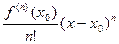меняет знак при переходе из правой в левую полуокрестность. Тогда 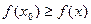и 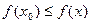в той или иной полуокрестности, и экстремума нет.

Замечание. Кстати, предыдущую теорему 4 можно было доказать таким же способом, n=2 это частный случай этой теоремы. Но там было показано более простое рассуждение, с помощью роста и убывания функции, чтобы было более понятно.