Уравнение касательной, формула Тейлора.
Уравнение касательной. 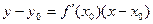
Доказательство.
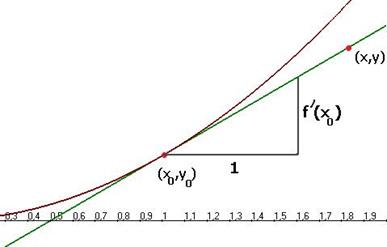
Рассмотрим треугольник. Его катеты 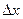 и
и 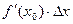 , так как тангенс угла наклона касательной это
, так как тангенс угла наклона касательной это 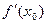 .
.
Направляющий вектор для прямой направлен в точности по гипотенузе.
При этом, мы можем пропорционально увеличить этот треугольник, тогда катеты будут такие: 1 и 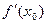 .
.
Соответственно, направляющим вектором можем считать такой вектор: 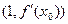 .
.
Возьмём теперь точку 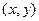 где-нибудь на касательной. Она принадлежит касательной в точности тогда, когда вектор
где-нибудь на касательной. Она принадлежит касательной в точности тогда, когда вектор 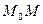 коллинеарен направляющему вектору этой прямой, т.е.
коллинеарен направляющему вектору этой прямой, т.е. 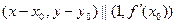 .
.
Запишем пропорцию координат так, как это всегда делали в теме «аналоитическая геометрия». Получается каноническое уравнения прямой: 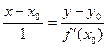 . А теперь просто умножим на
. А теперь просто умножим на 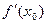 . Получается
. Получается 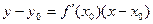 .
.
Замечание. Уравнение касательной можно запомнить в виде 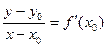 причём, так запомнить легче.
причём, так запомнить легче.
Пример.Найти касательную к графику 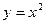 в точке
в точке 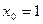
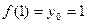 ,
, 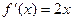 ,
, 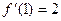 . Уравнение
. Уравнение 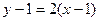 , то есть
, то есть 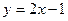 .
.
Если кривая задана неявно, то уравнение касательной в точке 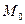 может быть тоже записано в виде:
может быть тоже записано в виде:
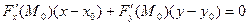
Доказательство.Рассмотрим кривую и точку 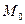 на ней. Градиент в этой точке ортогонален поверхности.
на ней. Градиент в этой точке ортогонален поверхности.
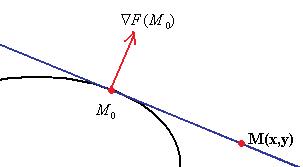
Тогда строим уравнение прямой так, как это делали в аналитической геометрии: вектор 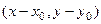 ортогонален
ортогонален 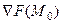 , то есть их скалярное произведение 0. Тогда получается именно такое уравнение:
, то есть их скалярное произведение 0. Тогда получается именно такое уравнение:
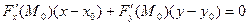 .
.
Дата добавления: 2016-12-26; просмотров: 1200;
