Барометрическая формула.

Распределение Больцмана для частиц во внешнем потенциальном поле

Газ, на который не действует внешнее силовое поле, равно­мерно заполняет объем, в котором он находится, благодаря хаотичности теплового движения молекул. Если на молекулы газа действуют внешние силы, то концентрация газа не будет одинаковой во всех точках объема. Рассмотрим в качестве примера атмосферный газ, находящийся в поле земного тяго­тения. Если бы отсутствовало тепловое движение, то все мо­лекулы атмосферы опустились бы на поверхность Земли под действием сил тяжести и земная атмосфера не могла бы суще­ствовать. Однако этому препятствует хаотическое движение молекул, которое способствует обратному процессу — стремле­нию атмосферного газа рассеяться и заполнить равномерно всю Вселенную. Следовательно, атмосфера Земли может существовать за счет этих двух факторов в некотором равновесном состоянии, при котором ее плотность, концентрация молекул и давление будут зависеть от пространственных ко­ординат.

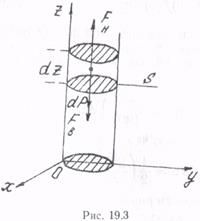
Найдем закон измене­ния этих величин в зависимости от высоты над поверхностью Земли. Бу­дем считать, что газ на­ходится в состоянии термодинамического равно­весия и его температура всюду одинакова. Выделим некоторый столб газа, имеющий форму цилиндра, площадью поперечного сече­ния s, и направим ось z вдоль столба по направлению от поверхности Земли. Установим начало отсчета координаты z на поверхности Земли (рис. 19.3).

Выделим на высоте z элементарный слой столба газа тол­щиной dz и воспользуемся тем, что этот слой, как и весь столб, находится в состоянии механического равновесия. Это значит, что равнодействующая всех сил, действующих на слой, равна нулю. Из рис. 19.3 видно, что равнодействующая складыва­ется из трех сил: две силы давления F_H и F_B, действующие на нижнее и верхнее основание слоя, и сила тяжести dP самого слоя. Обозначим давление газа в точках нижнего основания p, а в точках верхнего основания р+ dp. Тогда

F_H = pS; F_B = (p + dp)S; dP = ρgSdz,

где ρ — плотность слоя воздуха.

С учетом направления сил условие равновесия слоя запишется в виде

F_B+ dP = F_H(18.28)

или

(р + dp) S + ρgSdz = pS. (18.29)

Раскрыв в (18.29) скобки, получим дифференциальное уравнение

dp = —ρgdz. (18.30)

Из уравнения Клапейрона — Менделеева следует, что плотность газа связана с давлением формулой

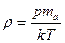, (18.31)

где т_а — масса молекулы газа.

Используя (18.31), преобразуем дифференциальное урав­нение (18.30) к виду

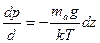. (18.32)

Интегрируя это уравнение по высоте от 0 до z, получаем

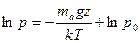, (18.33)

где ln p₀ — постоянная интегрирования.

Потенциируя (18.33), имеем

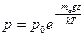. (18.34)

Из (18.34) видно, что р₀ имеет смысл давления атмосферы на поверхности Земли, где z = 0.

Полученное уравнение определяет зависимость давления атмосферы вблизи Земли от высоты над уровнем моря. Как и следовало ожидать, при увеличении высоты давление уменьшается. В соответствии с формулой (18.34), которая называется барометрической, это уменьшение подчиняется экспоненциальному закону. Измеряя давление по барометру, проградуированному в соответствии с барометрической фор­мулой, можно определить высоту объекта над поверхностью Земли. Такой прибор называется альтиметром и широко при­меняется в авиации.

Используя барометрическую формулу, легко установить закон распределения концентрации молекул по высоте h над поверхностью Земли. С этой целью воспользуемся уравнени­ем состояния идеального газа p= nkT. В этой формуле дав­ление р и концентрация молекул п зависят от высоты, в то время как температура Т постоянная в соответствии с пред­положением, что газ находится в состоянии термодинамиче­ского равновесия. Из уравнения состояния и барометрической формулы для концентрации п на высоте h вытекает:

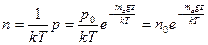, (18.35)

где n₀ — концентрация молекул воздуха при h = 0.

Обратив внимание на то, что в показатель экспоненты в правой части (18.35) входит потенциальная энергия моле­кулы в поле силы тяжести W_ПОТ = m_agh, перепишем (18.35) в виде

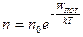. (18.36)

Оказывается, что выражение (18.36) для распределения молекул имеет общий характер и справедливо для частиц, находящихся во внешнем потенциальном поле любого вида. Это распределение называется распределением Больцмана.

В распределении Больцмана (18.36) под n₀ следует пони­мать концентрацию молекул в точке поля, где их потенциаль­ная энергия равна нулю, W_ПОТ = 0, а п представляет собой концентрацию молекул в точке, где их потенциальная энергия равна W_ПОТ.

Как известно, плотность газа ρ прямо пропорциональна концентрации молекул п. Поэтому, используя (18.35), нетруд­но показать, что распределение плотности воздуха в атмо­сфере Земли будет описываться выражением:

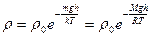, (18.37)

где М — молярная масса газа.

Из (18.34), (18.35) и (18.37) следует, что в атмосфере Земли р, п и ρ воздуха уменьшаются единообразно с увели­чением высоты.

Учитывая, что концентрация п по определению равна 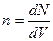, где dN — число молекул в элементарном объеме dV, можно представить распределение Больцмана в форме

.

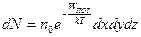Здесь под dN следует понимать число молекул, находя­щихся в элементарном объеме dV = dxdydz с координатами х, у, z и обладающих произвольными скоростями.

Учтем теперь, что молекулы газа, находящегося в состоя­нии термодинамического равновесия, распределены по скоро­стям в соответствии с (18.21) (распределение Максвелла). Это значит, что для того, чтобы определить число молекул dN газа в объеме dV со скоростями, попадающими в интервал dυ_x, dυ_y, dυ_z, следует учесть оба распределения. Мы приходим к формуле, которая называется распределением Максвелла — Больцмана:

.

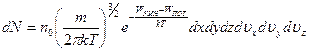Следует отметить, что распределение Максвелла — Больц­мана и сама его формулировка имеют смысл только в том случае, когда движение молекул подчиняется законам клас­сической физики. Если движение частиц носит квантовый ха­рактер, то имеют место другие распределения, о которых пойдет речь ниже.