Дифференциальные уравнения в полных дифференциалах
Определение. Дифференциальное уравнение первого порядка вида:
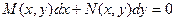
называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции 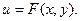
Интегрирование такого уравнения сводится к нахождению функции u, после чего решение находится в виде: 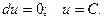
Таким образом, для решения надо определить:
1) в каком случае левая часть уравнения представляет собой полный дифференциал функции u;
2) как найти эту функцию.
Если дифференциальная форма 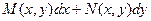 является полным дифференциалом некоторой функции u, то можно записать:
является полным дифференциалом некоторой функции u, то можно записать:
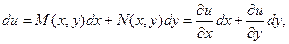
т.е. 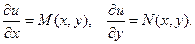
Найдем смешанные производные второго порядка, продифференцировав первое уравнение по у, а второе – по х:
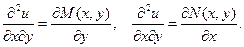
Приравнивая левые части уравнений, получаем необходимое и достаточное условие того, что левая часть дифференциального уравнения является полным дифференциалом:
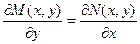 .
.
Рассмотрим вопрос о нахождении функции u.
Проинтегрируем равенство 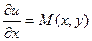 :
:
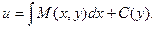
Определим функцию 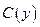 . Продифференцируем полученное равенство по у:
. Продифференцируем полученное равенство по у:
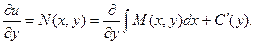
Откуда получаем: 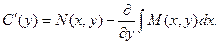
Для нахождения функции 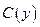 необходимо проинтегрировать приведенное выше равенство. Однако перед интегрированием необходимо доказать, что функция
необходимо проинтегрировать приведенное выше равенство. Однако перед интегрированием необходимо доказать, что функция 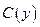 не зависит от х. Это условие будет выполнено, если производная этой функции по х равна нулю:
не зависит от х. Это условие будет выполнено, если производная этой функции по х равна нулю:
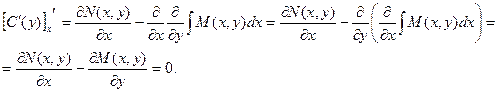
Теперь определяем функцию 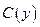 :
:
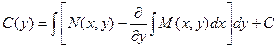 .
.
Подставляя этот результат в выражение для функции u, получаем:
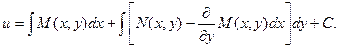
Общий интеграл исходного дифференциального уравнения будет иметь вид:
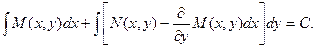
Заметим, что при решении уравнений в полных дифференциалах не обязательно использовать полученную формулу. Решение может получиться более компактным, если просто следовать методу, которым была получена формула.
Пример. Решить уравнение 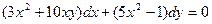 .
.
Проверим условие полных дифференциалов: 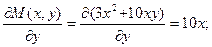
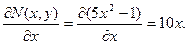
Условие полных дифференциалов выполняется, следовательно, исходное дифференциальное уравнение является уравнением в полных дифференциалах. Определяем функцию u.
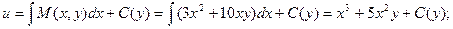
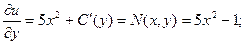
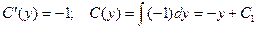 .
.
Таким образом, 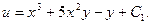
Находим общий интеграл исходного дифференциального уравнения:
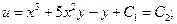
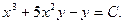
9. Дифференциальные уравнения вида 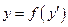 и
и 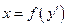
Решение уравнений, не содержащих в одном случае аргумента х, а в другом – функции у, ищем в параметрической форме, принимая за параметр производную неизвестной функции:
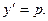
Для уравнения первого типа получаем: 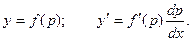
Делая замену, получаем: 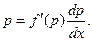
В результате этих преобразований получаем дифференциальное уравнение с разделяющимися переменными:
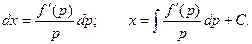
Общий интеграл в параметрической форме представляется системой уравнений:
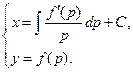
Исключая из этой системы параметр р, получим общий интеграл и не в параметрической форме.
Для дифференциального уравнения вида 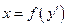 с помощью той же самой подстановки и аналогичных рассуждений получаем результат:
с помощью той же самой подстановки и аналогичных рассуждений получаем результат:
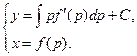
Дата добавления: 2016-05-05; просмотров: 910;
