Дифференциальные исчисления функций одной переменной

Основные формулы:

Производная от функции у=f(х) по аргументу х

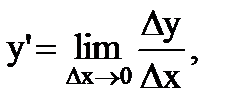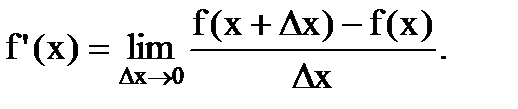или (6.3.4)

Формулы дифференцирования основных функций:

1.(хm)'=mxm–1.	11.(ctg x)'=–cosec2x.
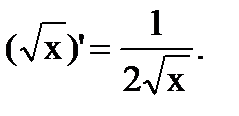
2.	12. (arcsin x)'=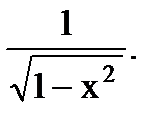
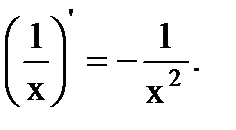
3.	13.(arccos x)'=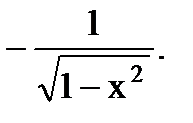
4. (ex)'=ех.	14. (arctg x)'=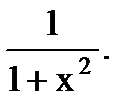
5. (аx)'=ахln a.	15. (arcсtg x)'= –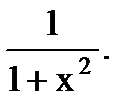
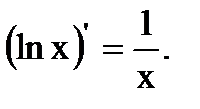
6.	16.(s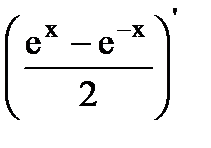h x)'= =ch x.
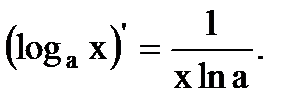
7.	17. (c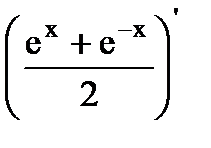h x)'= =sh x.
8. (sin x)'=cos x.	18. (th x)'=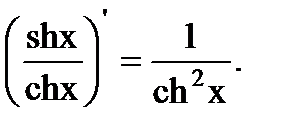
9. (cos x)'=–sin x.	19. (cthx)'=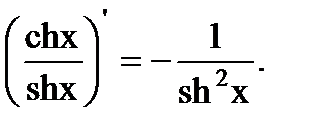
10. (tgx)'=sec2x.

Основные правила дифференцирования

Пусть С–постоянная, u=u(x), v=v(x) – функции, имеющие производные. Тогда:

1) С'=0; 2) х'=1; 3) (u'±v')= u'±v'; 4) (Сu)'=Сu'; 5) (uv)'=u'v+ uv';

6) 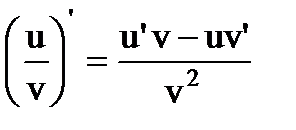; 7) если y=f(x), u=u(x), т.е. у=f[u(x)], то

у'_х= у'_u∙ u'_х.

Дифференцирование функций заданных параметрически: х=φ (t), y=ψ(t).

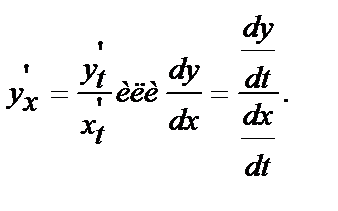(6.3.5.)

Уравнение касательной к кривой у=f(х) в точке М₀(х₀;у₀): у–y₀=y'₀(х–х₀).

Уравнение нормали: у–y₀= 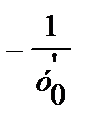(х–х₀).

Угол между двумя кривыми у=f₁(х) и у=f₂(х) в точке их пересечения М₀(х₀;у₀)

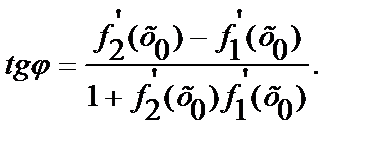(6.3.6.)

Производная n-го порядка от функции у=f(x): у⁽ⁿ⁾=(у^(n–1))', обозначение: у⁽ⁿ⁾, f⁽ⁿ⁾ (x), .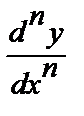

Дифференциалы высших порядков: dy=y'dx.

Основные свойства дифференциала:

1. dC=0, где С=const.

2. d(Cu)=Cdu.

3. d(u±v)=du±dv.

4. d(uv)=udv+vdu.

5.

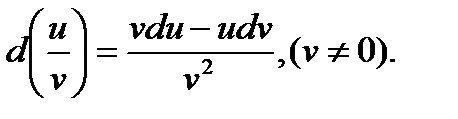
6. df(u)=f'(u)du.

Дифференциал n-го порядка: dⁿy=d(d^n–1y).

Теорема Лагранжа 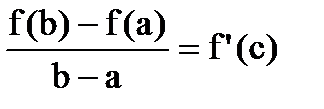. (6.3.7.)

Теорема Коши 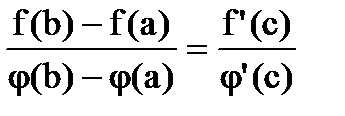. (6.3.8.)

Правило Лопиталя раскрытия неопределенностей 0/0, ∞/∞:

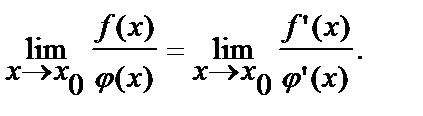(6.3.9)

Пример 6.3.2.у=(sinx)­^tgx.

Решение.

Имеем ln у=tgx∙lnsinx, откуда

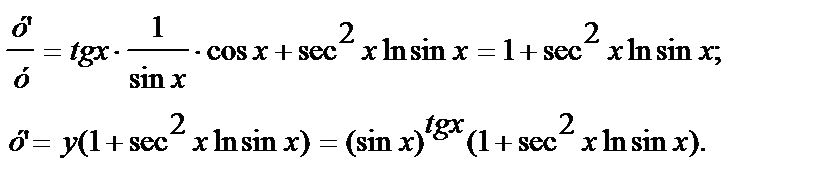
Пример 6.3.3.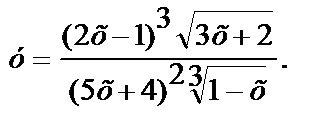

Решение.

Здесь заданную функцию следует предварительно прологарифмировать:

ln y=3 ln (2x-1) + 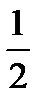ln (3x+2)-2ln(5x+4) - 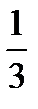ln(1-x);

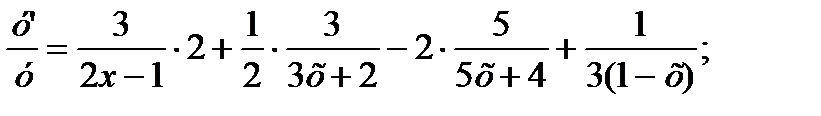
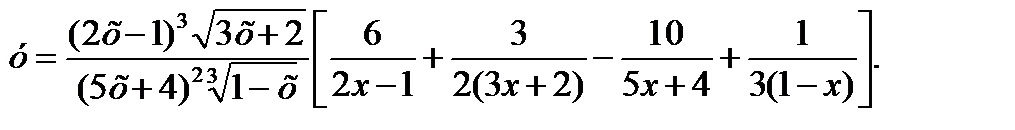
Пример 6.3.4.Найти дифференциалы первого, второго и третьего порядков функции у=(2х–3)³.

Решение.

dy=3(2x–3)²∙2dx=6(2x–3)²dx,

d²y=12(2x–3)²∙2dx²=24(2x–3)dx²,

d³y=24∙2dx³=48dx³.