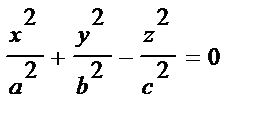Поверхности II порядка. Канонические уравнения
| Название поверхности | Каноническое уравнение | ||
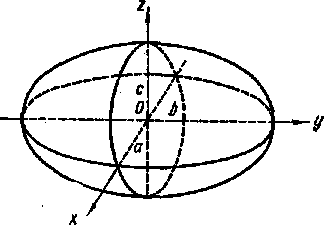
| эллипсоид | 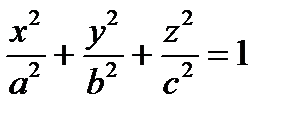 (рис.1) (рис.1)
| ||
| гиперболоиды | однополостный гиперболоид | 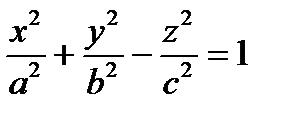 (рис.2) (рис.2)
| |
| двуполостный гиперболоид |  (рис.4) (рис.4)
| ||
| конус | 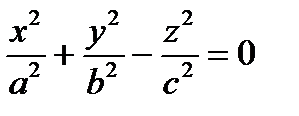 (рис.5) (рис.5)
| ||
| пароболоиды | эллиптический параболоид | 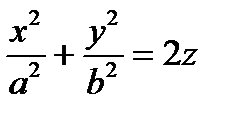 (рис.3) (рис.3)
| |
| гиперболический параболоид | 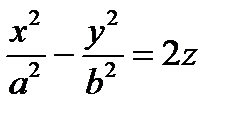 (рис.6) (рис.6)
| ||
| цилиндры | эллиптический цилиндр | 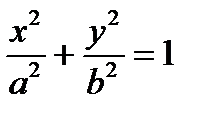
| |
| гиперболический цилиндр | 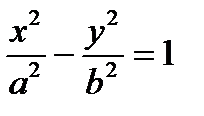
| ||
| параболический цилиндр | 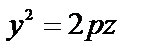
| ||
| пара плоскостей | левая часть уравнения распадается на произведение двух линейных множителей |
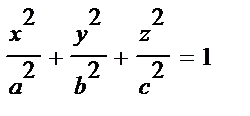
|
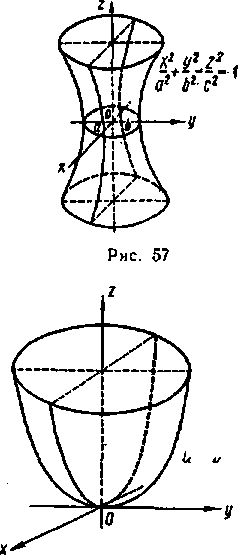
Рисунок 6.2.2
Рисунок 6.2.1.

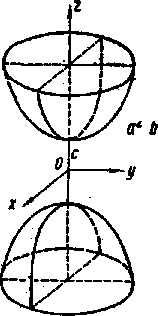

Рисунок 6.2.3.
Рисунок 6.2.4.
|
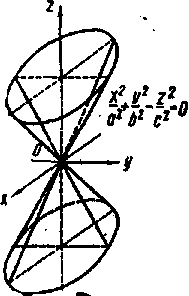
|
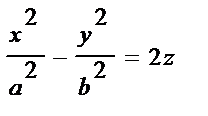
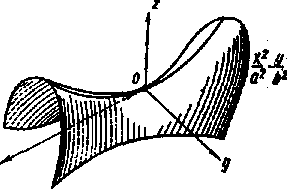
Рисунок 6.2.6.
Рисунок 6.2.5.
Введение в математический анализ
Пределы функций
При вычислении предела элементарной функции f(x) приходится сталкиваться с двумя существенно различными типами примеров.
1 Функция f(x) определена в предельной точке x=a. Тогда
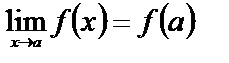 . (6.3.1)
. (6.3.1)
2 Функция f(x) в предельной точке х=а не определена или же вычисляется предел функции при 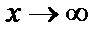 . Тогда вычисление предела требует в каждом случае индивидуального подхода. В одних случаях (наиболее простых) вопрос сводится непосредственно к применению теорем о свойствах бесконечно больших и бесконечно малых функций и связи между ними. Более сложными случаями нахождения предела являются такие, когда функция f(x) в точке х=а или при
. Тогда вычисление предела требует в каждом случае индивидуального подхода. В одних случаях (наиболее простых) вопрос сводится непосредственно к применению теорем о свойствах бесконечно больших и бесконечно малых функций и связи между ними. Более сложными случаями нахождения предела являются такие, когда функция f(x) в точке х=а или при 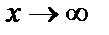 представляет собой неопределенность
представляет собой неопределенность
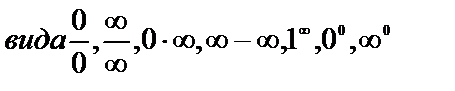 .
.
Приведем основные теоремы, на которых основано вычисление пределов.
1 Если существуют  и
и 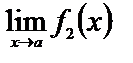 , то
, то
а)  ;
;
б) 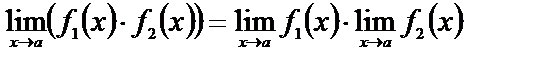 ;
;
Частные случаи:
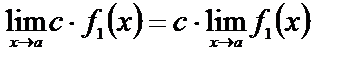
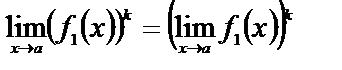
в) 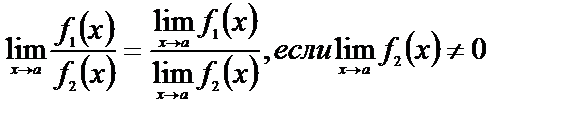 .
.
2 Если в некоторой окрестности точки х=а (кроме, быть может, точки а) выполнено условие f(x)=q(x) и если предел одной из этих функций в точке а существует, то
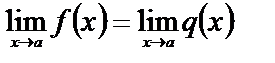 .
.
3 Если существует 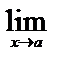 U(х) и f(х) – элементарная функция, то
U(х) и f(х) – элементарная функция, то
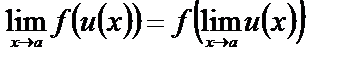 .
.
Например : 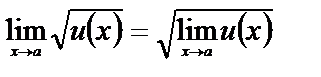 ,
,
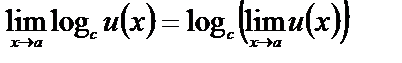 .
.
4 Первый замечательный предел: 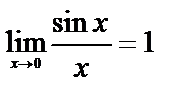 . (6.3.2)
. (6.3.2)
5 Второй замечательный предел: 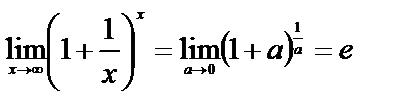 . (6.3.3)
. (6.3.3)
Также при вычислении пределов следует знать ряд эквивалентных бесконечно малых функций:
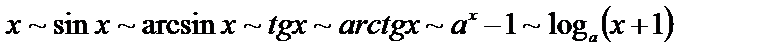 при
при 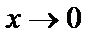
Примеры 6.3.1.
Вычислите пределы:
1)  .
.
Функция f(x) в предельной точке х=2 не определена; так как числитель и знаменатель дроби обращается в нуль, то имеем неопределенность вида 0/0.
Преобразуем дробь, и по формуле (1) получим
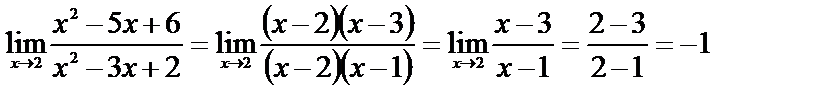 .
.
2) 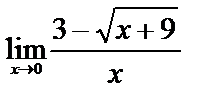 .
.
В этом случае также получается неопределенность вида 0/0. Преобразование функции сводится к уничтожению иррациональности в числителе: для этого умножим числитель и знаменатель на выражение 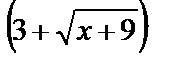 и затем сократим дробь на
и затем сократим дробь на 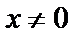 . Отсюда
. Отсюда
 .
.
3)  .
.
Здесь имеет место неопределенность вида 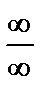 . Разделим числитель и знаменатель на
. Разделим числитель и знаменатель на 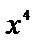 (наивысшую степень х в данной дроби). Тогда
(наивысшую степень х в данной дроби). Тогда
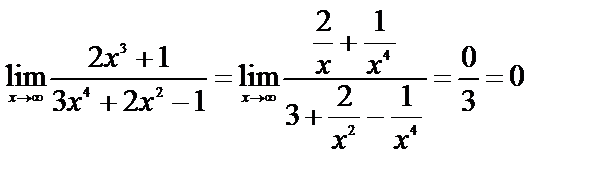 .
.
4) 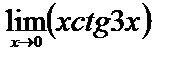 .
.
Здесь получается неопределенность вида 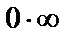 . Представим функцию в виде дроби, которая в точке х=0 дает неопределенность вида 0/0, после чего преобразуем её так, чтобы можно было воспользоваться первым замечательным пределом:
. Представим функцию в виде дроби, которая в точке х=0 дает неопределенность вида 0/0, после чего преобразуем её так, чтобы можно было воспользоваться первым замечательным пределом:
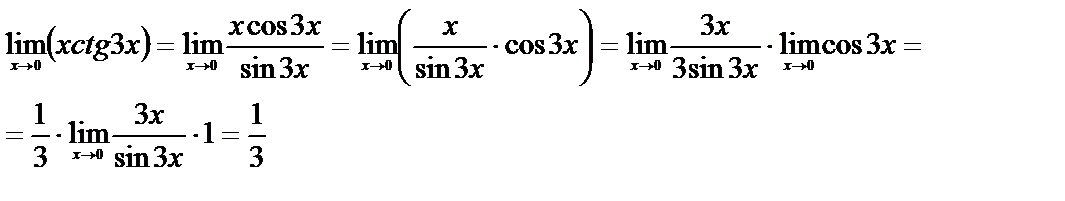
5) 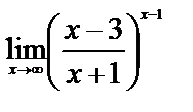
Функция 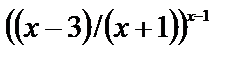 при x->
при x-> 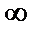 представляет собой степень, основание которой стремится к единице, а показатель – к бесконечности, неопределенность вида
представляет собой степень, основание которой стремится к единице, а показатель – к бесконечности, неопределенность вида 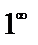 .
.
Преобразуем функцию таким образом, чтобы использовать второй замечательный предел:
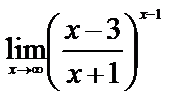 =
= 
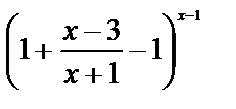 =
= 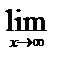
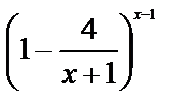 = =
= = 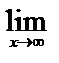
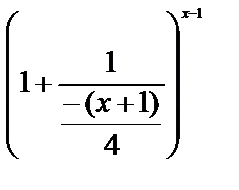 =
= 
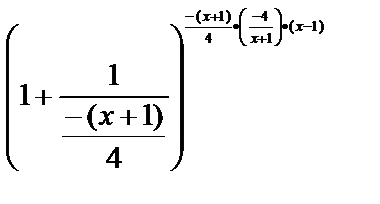 =
=
= 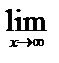
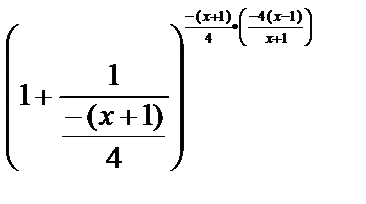 =
= 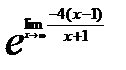 =
= 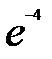
6) 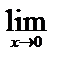
 .
.
Используя второй замечательный предел, находим
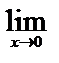
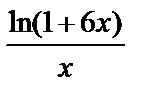 =
= 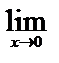

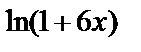
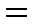
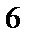
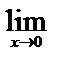
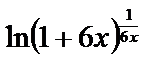
 =
= 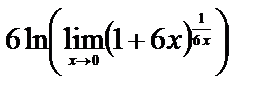 =
= 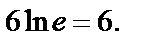
Дата добавления: 2016-10-17; просмотров: 1060;