Дифференциальные уравнения первого порядка.

Определение: дифференциальное уравнение первого порядка называют разрешенным относительно производной, если оно представлено в виде: .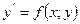

Задачей Коши для дифференциального уравнения первого порядка называют задачу о нахождении частного решения дифференциального уравнения, удовлетворяющего начальному условию: .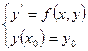

Теорема Коши (о существовании и единственности решения задачи Коши).

Если в некоторой области 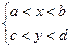функция 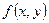является непрерывной, а ее частная производная 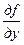ограничена, то для любой точки 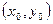из этой области существует единственное решение задачи Коши: .

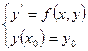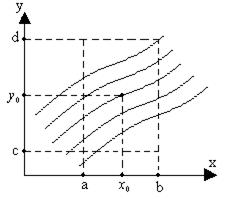
Другими словами, через каждую точку 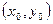из данной области проходит единственная интегральная кривая, соответствующая решению задачи Коши.

Поскольку производная имеет смысл тангенса угла наклона касательной, значение функция 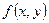в каждой точке равно тангенсу угла наклона касательной, проведенной к интегральной кривой. Те линии, для которых это значение одно и то же, называются изоклинами.