Аффинная классификация кривых второго порядка.

Теорема 5.5. Любая кривая второго порядка аффинно эквивалентна одной из 9 кривых, приведенных в таблице. Приведенные кривые аффинно не эквивалентны между собой.

Название кривой	Каноническое уравнение кривой	Расширенная матрица	rgA	S(A)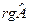
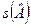
Эллипс		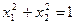diag(1,1,-1)
Мнимый эллипс		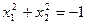diag(1, 1, 1)
Гипербола		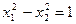diag(–1, 1, –1)
Пара пересекающихся мнимых прямых		diag(0, 1, 1)
Пара пересекающихся прямых	,	diag(0, 1, –1)
Парабола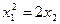
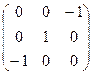
Пара параллельных прямых		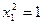diag(–1, 1, 0)
Пара параллельных мнимых прямых		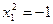diag(1, 1, 0)
Пара совпавших параллельных прямых		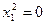diag(0, 1, 0)

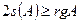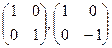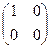Доказательство. Любую кривую 2-го порядка в соответствующих аффинных координатах можно описать одним из перечисленных канонических уравнений. Действительно, и rgA может принимать лишь два значения 1 или 2, поэтому матрица A может иметь один из следующих трёх видов: или . Очевидно, приведённая таблица исчерпывает все возможные варианты расширенных матриц, соответствующих каждой из трёх матриц A.