Изменение матрицы линейного оператора при изменении базиса.

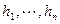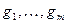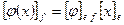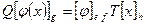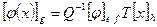Получим формулу изменения матрицы линейного оператора при изменении базиса в пространствах V и W. Пусть новый базис W, а новый базис V. Координаты вектора в разных базисах связаны матрицей перехода. Пусть [x]_e=T[x]_h и [y]_f=Q[y]_g. Отсюда и равенства выводим или . Сопоставляя полученное равенство с 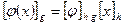, получаем равенство матриц .

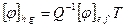Алгебра линейных операторов.

Обозначим через 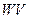множество линейных операторов, действующих из пространства W в пространство V. На множестве 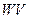определим операции умножения оператора на скаляр 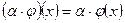и сложение операторов 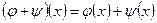. Оператор назовем нулевым, если все векторы переводятся в ноль. Нулевой оператор обозначим через 0, т.е 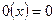. Относительно операций умножения на скаляр и сложения множество линейных операторов 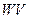образует линейное пространство. Отметим, что 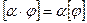и .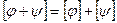

Пусть W,V,U – линейные пространства над полем P, а 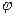линейный оператор из W в V, 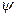- линейный оператор из V в U. Отображение 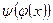из W в U является линейным оператором и обозначается 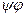. Пусть 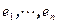- базис W, 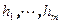- базис V, 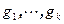- базис U, тогда .

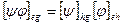Простейший вид матрицы линейного оператора.