Эквивалентность матриц

Матрицы A и B называются эквивалентными, если найдутся невырожденные матрицы Q и T, что A=QBT.

Теорема 6.1. Если матрицы эквивалентны, то их ранги равны.

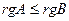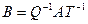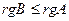Доказательство. Поскольку ранг произведения не превосходит ранги сомножителей, то . Так как , то . Объединяя два неравенства, получаем требуемое утверждение.

Теорема 6.2. Элементарными преобразованиями со строками и столбцами матрицу A можно привести к блочному виду 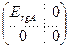, где 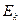- единичная матрица порядка k, а 0 – нулевая матрица соответствующих размеров.

Доказательство. Приведем алгоритм приведения матрицы A к указанному виду. Номера столбцов будут указываться в квадратных скобках, а номера строк – в круглых скобках.

1. Положим r=1.

2. Если 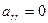то перейдем на шаг 4, иначе перейдем на шаг 3.

3. Сделаем преобразования со строками 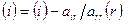, где i=r+1,…,m, и со столбцами 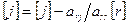, где j=r+1,…,n, и 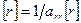. Увеличим r на 1 и вернемся на шаг 2.

4. Если 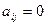, при i=r+1,…,m, j=r+1,…,n, то конец. В противном случае найдем i,j>r, что 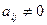. Переставим строки 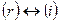и столбцы 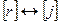, вернемся на шаг 2.

Очевидно, что алгоритмом будет строиться последовательность эквивалентных матриц, последняя из которых имеет требуемый вид.

Теорема 6.3. Матрицы A и B одинаковых размеров эквивалентны тогда и только тогда, когда их ранги равны.

Доказательство. Если матрицы эквивалентны, то их ранги равны (Теорема 6.1). Пусть ранги матриц равны. Тогда найдутся невырожденные матрицы, что 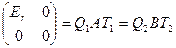, где r=rgA=rgB (Теорема 6.2). Следовательно, 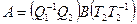, и матрицы A и B – эквивалентны.

Результаты данного пункта позволяют находить простейший вид матрицы линейного оператора и базисы пространств, в которых матрица линейного оператора имеет этот простейший вид.