Линейный оператор. Матрица линейного оператора.
Пусть W и V линейные пространства над числовым полем P. Однозначное отображение 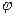 линейного пространства W в линейное пространство V называется линейным оператором, если для любых векторов x,y из W и чисел
линейного пространства W в линейное пространство V называется линейным оператором, если для любых векторов x,y из W и чисел 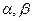 из поля P справедливо равенство
из поля P справедливо равенство 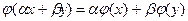 .
.
Примеры линейных операторов.
- Линейная функция
- Дифференцирование функций
- Проекция вектора
- Пседообратная матрица
Матрица линейного оператора.
Пусть 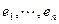 базис W. Разложим вектор x из W по этому базису
базис W. Разложим вектор x из W по этому базису 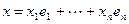 и найдем его образ
и найдем его образ 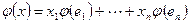 . Из полученного равенства видно, что образ вектора определяется координатами вектора и значениями линейного оператора на базисных векторах. Обозначим через
. Из полученного равенства видно, что образ вектора определяется координатами вектора и значениями линейного оператора на базисных векторах. Обозначим через 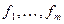 базис V. Координаты вектора x из W в базисе
базис V. Координаты вектора x из W в базисе 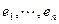 обозначим через
обозначим через 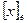 , а координаты вектора y из V в базисе
, а координаты вектора y из V в базисе 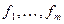 обозначим через
обозначим через 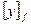 . Перейдем в последнем равенстве от равенства векторов к равенству их координат
. Перейдем в последнем равенстве от равенства векторов к равенству их координат 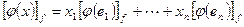 , которое можно записать используя матричное умножение следующим образом
, которое можно записать используя матричное умножение следующим образом 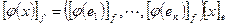 . Матрица
. Матрица 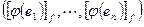 называется матрицей линейного оператора и обозначается
называется матрицей линейного оператора и обозначается 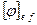 .
.
Дата добавления: 2016-05-25; просмотров: 1023;
