Приведение уравнения квадрики к простейшему виду

Теорема 5.3 Для любого уравнения квадрики 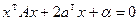найдется аффинная замена системы координат, приводящую квадрику к виду .

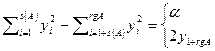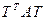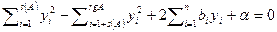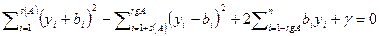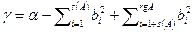Доказательство. По теореме Лагранжа существует невырожденная матрица T, приводящая матрицу А к нормальному виду, т.е. - диагональная матрица, по главной диагонали которой расположено s(A) единиц и rgA-s(A) минус единиц. После замены координат x=Ty получим уравнение квадрики . Преобразуем уравнение , где . Положим 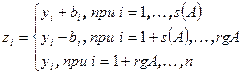. В новой системе координат уравнение квадрики имеет вид .

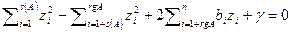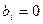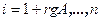Если , где , то 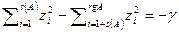, и теорема в этом случае доказана. Пусть найдется i, при котором выполняется неравенство 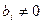. Если i=1+rgA, то сделаем аффинную замену координат 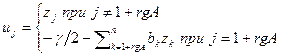, а если i>1+rgA, то замену 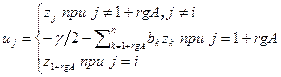. В результате получим уравнение квадрики 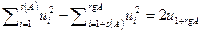, что и требовалось доказать.

Если уравнение квадрики умножить на не нулевое число, то множество решений уравнения не изменится. Два уравнения квадрики называются аффинно-эквивалентными, если от одного к другому можно перейти в результате аффинного преобразования или умножения уравнения на произвольное ненулевое число.

Теорема 5.4 Уравнение квадрики аффинно эквивалентно одному из следующих уравнений 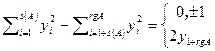, причем 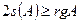. Если 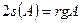, то правая часть не может равняться -1. Все эти уравнения аффинно не эквивалентны между собой.

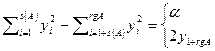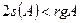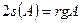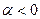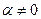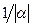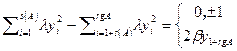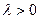Доказательство. Аффинной заменой координат любое уравнение приводится к виду . Если , то умножим уравнение на -1. Аналогично, если и , то умножим уравнение на -1. Если , то умножим уравнение на . В результате этих преобразований получим уравнение вида , где и 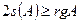. Причем, если 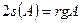, то правая часть уравнения не может равняться -1. Сделаем замену координат 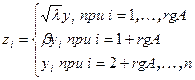и получим одно из уравнений квадрики, приведенных в условии теоремы.

Рассмотрим матрицы 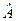для уравнений квадрик, приведенных в условии теоремы. Для квадрики 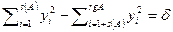, где 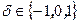, расширенная матрица 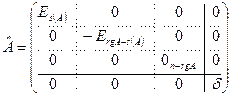, а для квадрики 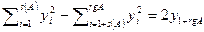расширенная матрица 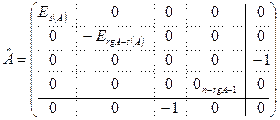. Приведем таблицу аффинных инвариантов (Следствие 5.2).

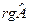
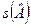
		квадрика
rgA	s(A)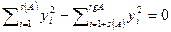
1+rgA	s(A)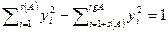
1+rgA	s(A)+1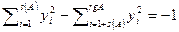
2+rgA	s(A)+1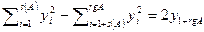

Поскольку все наборы инвариантов различны, то теорема доказана.