Закон инерции квадратичных форм.

Теорема 4.4 Закон инерции. Для любой эрмитовой билинейной функции нормальный вид определяется единственным образом.

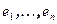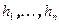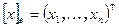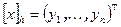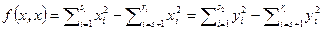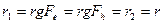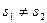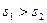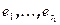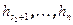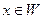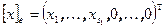Доказательство проведем методом от противного. Пусть найдется два базиса и , в которых нормальный вид различный. Пусть и и . Поскольку , то нормальный вид различен только если . Для определенности положим . Обозначим через W линейную оболочку векторов , а через U – линейную оболочку векторов . Для не нулевого вектора имеем и 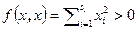, а для вектора 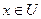выполняются равенства 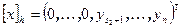и 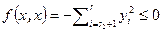. Пересечение подпространств 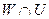не может содержать векторов отличных от нуля, но 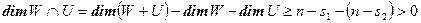. К полученному противоречию привело допущение 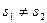. Таким образом теорема доказана.

Число положительных слагаемых в нормальном виде эрмитовой формы называется положительным индексом инерции, а число слагаемых с отрицательными коэффициентами – отрицательный индекс инерции. Индексы инерции эрмитовых форм не зависят от выбора базиса.

Теорема Якоби

Обозначим через 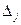угловой минор j-го порядка матрицы F (и положим ).

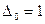Теорема 4.5 Якоби. Пусть 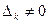(k=1,2,..,r). Существует канонический базис 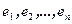, для которого 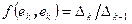, при k=1,2,..,r, и 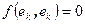при k>r.

Доказательство очевидным образом повторяет Следствие 4.6.