Приведение квадратичных форм к нормальному виду элементарными преобразованиями

Симметричные матрицы A и F назовем конгруэнтными, если найдется невырожденная матрица P, что 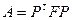. Матрицы билинейной формы в различных базисах конгруэнтны. Из теоремы Лагранжа вытекает, что симметричная квадратная матрица конгруэнтна диагональной матрице diag(1,…,1.-1,…,-1,0,…,0). Опишем алгоритм приведения симметричной квадратной матрицы F к диагональному виду элементарными преобразованиями. Отметим, если мы совершаем какие то действия со строками матрицы F, то те же самые действия надо совершить и со столбцами матрицы. Номера столбцов будут указываться в квадратных скобках, а номера строк – в круглых скобках.

1. Положим r=1.
2. Если 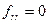, то перейдем на шаг 4, иначе шаг 3.
3. Положим 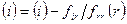, , 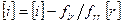где 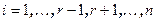. Затем увеличим r на 1 и вернемся на шаг 2.
4. Если найдется i, что 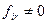, то положим 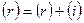, 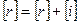и вернемся на шаг 2. В противном случае перейдем на шаг 5.
5. Если для всех i,j>r справедливо неравенство 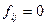, то алгоритм работу закончил. В противном случае найдутся номера i,j, для которых 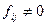. Тогда переставим строки 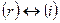и столбцы 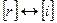и вернемся на шаг 2.

Легко проверить, что предложенный алгоритм построит диагональную матрицу конгруэнтную исходной матрице. Преобразованиями вида 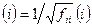, 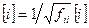можно добиться, чтобы на главной диагонали стояли только 0,1,-1. Перестановками строк и столбцов элементы матрицы, стоящие по главной диагонали, можно расположить в порядке не возрастания.

Если приписать справа единичную матрицу, то элементарные преобразования можно запомнить в ней.