Критерий Сильвестра.

Эрмитовая форма 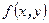называется положительно определенной, если для любого 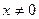справедливо неравенство .

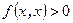Теорема 4.6 Критерий Сильвестра положительной определенности. Эрмитова форма положительна определена тогда и только тогда, когда все ее главные миноры (расположенные по главной диагонали) строго больше нуля.

Доказательство. Если все главные миноры F строго больше нуля, то и все угловые миноры матрицы F строго больше нуля. По теореме Якоби найдется базис, в котором эрмитова форма имеет вид 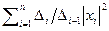. Поскольку все коэффициенты строго больше нуля, то эрмитова форма положительно определена.

Покажем обратное. Допустим, найдется главный минор матрицы F, не больше нуля. Не нарушая общности можно считать, что это угловой минор порядка k, так как в противном случае перенумеруем переменные соответствующим образом. Далее, можно считать, что все угловые миноры до (k-1)-го порядка больше нуля. Действительно, иначе можно положить k равным меньшему значению. Положим все переменные с номером больше k равными нулю. В результате получим эрмитову форму от k переменных с матрицей 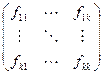. Угловые миноры этой матрицы до (k-1)-го порядка больше нуля, и, значит можно воспользоваться теоремой Якоби. В некотором базисе эта форма имеет вид 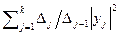. По построению 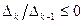, и, значит, найдется не нулевой вектор, значение эрмитовой формы 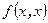на котором не больше нуля, что противоречит ее положительной определенности. К полученному противоречию привело допущение о существовании не положительных главных миноров матрицы F. Следовательно, все главные миноры больше нуля.

Квадрики.