Алгебраический критерий устойчивости Гурвица

Для оценки устойчивости линейной системы по критерию Гурвица необходимо из коэффициентов характеристиче­ского уравнения (3.5) составить определитель Гурвица, размерность которого равна порядку системы.

Определитель Гурвица имеет вид:

. (3.8)

Порядок составления определителя Гурвица следующий. В качестве элемента первого столбца первой строки определителя записывается коэффици­ент a_n-1, а затем на главной диагонали располагаются коэффициенты характеристического уравнения (3.4) с последовательно убывающими индексами. При этом в послед выражении нем столбце последней строки определителя записывается коэффициент .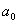

Затем, начиная от коэффициентов, стоящих на главной диагонали, заполняются столбцы определителя так, чтобы ин­дексы коэффициентов, расположенных над коэффициентами главной диагонали, последовательно убывали, а коэффициентов, расположенных под диагональными коэффициентами, – последовательно возрастали. Если в процессе заполнения столбца определителя индекс коэффициента достигает значения n или 0, то дальнейшее заполнение столбца осуществляется нулями.

Далее необходимо вычислить значение определителя Гурвица и всех его диагональных миноров, которые получают из определителя (3.8) путем отчеркивания равного числа строк и столбцов в левом верхнем углу определителя. Например, диагональный минор первого порядка равен Δ₁ = a_n-1; диагональный минор второго порядка:

Δ₂ = 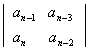, (3.9)

а диагональный минор третьего порядка:

Δ₃ = 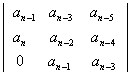. (3.10)

Очевидно, что диагональный минор n-го порядка совпадает с определителем Гурвица.

Линейная система устойчива, если при выполнении необходимого условия (3.6), определитель Гурвица и все его диагональные миноры будут положительны.

Пример нахождения минора:

Например, есть матрица:

Предположим, надо найти дополнительный минор M₂₃. Этот минор - определитель матрицы, получающейся путем вычеркивания строки 2 и столбца 3:

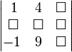
Получаем M₂₃ = 13

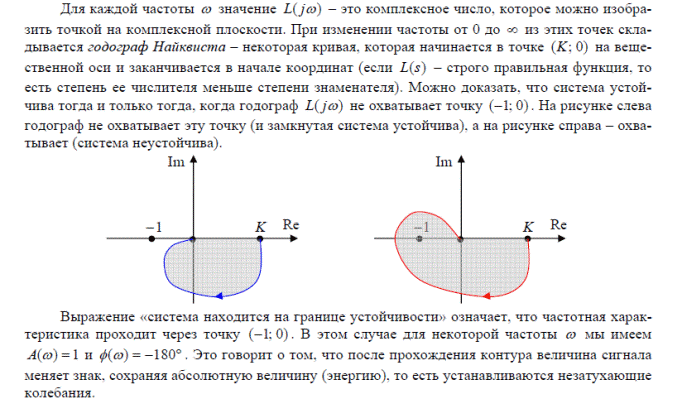
Частотные критерии устойчивости: Критерий Найквиста.