Импульсная - функция.

В качестве тестового сигнала можно, в принципе, использовать любой сигнал. Например, можно изучать реакцию системы на прямоугольный импульс. Вопрос в том, чтобы определить некоторый стандартный вид этого импульса. На рисунках а)-в) показаны три импульса, имеющих одинаковые площади. Для простоты будем считать, что эта площадь равна единице.

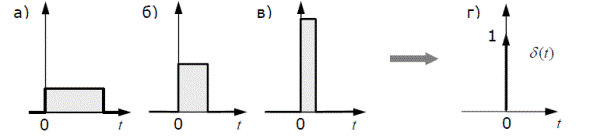
Что будет, если мы будем уменьшать ширину импульса, сохраняя его площадь? Очевидно, что высота импульса будет расти и в пределе (когда ширина стремится к нулю) станет бесконечной. Таким образом, мы получили еще один классический тестовый сигнал – единичный импульс или дельта-функцию Дирака δ(t) . Это идеальный (невозможный в реальной жизни) сигнал, который равен нулю во всех точках, кроме t = 0 , где он уходит к бесконечность, при чем его площадь (интеграл по всей оси времени) равен единице:

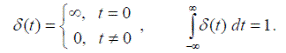
Поскольку бесконечный импульс невозможно нарисовать, на графике он изображается стрелкой, высота которой равна единице (см. рисунок г).

Иногда определяют дельта-функцию как производную от единичного ступенчатого сигнала 1(t) . Действительно, эта производная равна нулю при всех значениях t , кроме нуля, где она обращается в бесконечность. Реакция системы на единичный импульс (дельта-функцию) называется импульсной характеристикойи обозначается w(t):

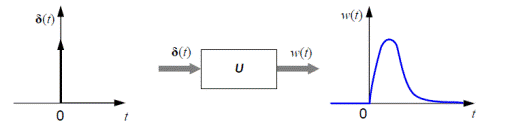
Импульсная характеристика, так же, как и переходная характеристика, определяется при нулевых начальных условиях, то есть, объект должен находиться в состоянии покоя.