Классификация систем автоматического управления

Все системы автоматического управления и регулирования делятся по различным признакам на

следующие основные классы:

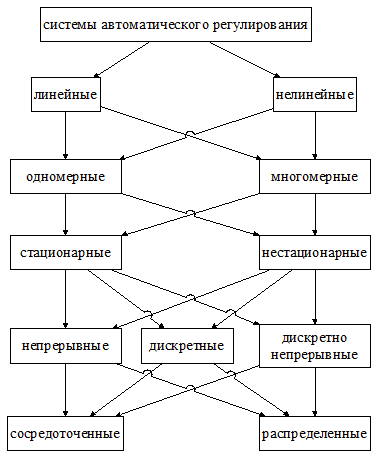
1. По основным видам уравнений динамики процессов управления:

а) линейные системы;

б) нелинейные системы.

2. По количеству управляющих параметров: одномерные (одноканальные) и многомерные (многоканальные).

3. По характеру представления сигналов различают:

а) непрерывные системы;

б) дискретные системы, среди которых выделяют импульсные, релейные, цифровые.

4. По характеру процессов управления:

а) детерминированные системы – системы с определенными переменными и процессами;

м

5. По характеру функционирования.

В зависимости от того, по какому закону изменяется заданное значение регулируемой величины,

системы автоматического управления подразделяются на:

а) системы стабилизации, поддерживающие постоянство регулируемой величины, т.е. yзад(t) = const;

б) системы программного регулирования, в которых заданное значение регулируемой величины изменяется по определенной заранее временной программе;

в) следящие системы, в которых заданное значение регулируемой величины изменяется в соответствии с состоянием некоторого заданного вектора переменных во времени;

г) системы оптимального управления, в которых показатель эффективности зависит не только от текущих значений координат но также от характера их изменения в прошлом, настоящем и будущем. Нахождение оптимального управления предполагает решение достаточно сложной математической задачи соответствующими методами, кроме того органической составной частью системы является компьютер;

д) адаптивные системы, в которых автоматически изменяются значения yзад , собственные параметры или структура при непредвиденных изменениях внешних условий на основании анализа состояния или поведения системы так, чтобы сохранялось заданное качество ее работы.

Системы с изменением заданного значения регулируемой величины называют экстремальными, с изменением параметров – самонастраивающимися, с изменением структуры – самоорганизующимися.

Математическое описание одномерных элементов и систем автоматического управления. Общие положения. Передаточные функции.

3.1. Общие положения.

Одномерными являются системы, которые имеют одну входную и одну выходную величину. Так как в электроэнергетике большинство систем являются одномерными, рассмотрим их математическое описание более подробно.

Поведение САУ в процессе функционирования представляют собой объединение статических и динамических режимов. Для проведения теоретических исследований САУ и её отдельных элементов необходимо иметь уравнения, которые описывают их поведение при внешних воздействиях, которые изменяются. Эти уравнения представляют собой выраженные в математической форме соотношения, которые связывают входные и выходные сигналы и воздействия.

С целью упрощения получения математических соотношений обычно вводят следующие допущения:

- САУ и её элементы имеют свойство стационарности.

- элементы САУ линейные

- процессы, протекающие в системе, являются непрерывными функциями времени при нулевых начальных условиях.

3.2. Математические модели. Линеаризация.

Во-первых, математические модели могут быть получены теоретически из законов физики(законы сохранения массы, энергии, импульса). Эти модели описывают внутренние связи в объекте и, как правило, наиболее точны.

Рассмотрим RLC-цепочку, то есть последовательное соединение резистора с сопротивлением R, катушки индуктивности с индуктивностью L и конденсатора с емкостью C. Она может быть описана с помощью двух уравнений:

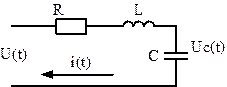
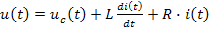
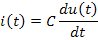
Второй способ – построение модели в результате наблюдения за объектомпри различных входных сигналах (этим занимается теория идентификации). Объект рассматривается как «черный ящик», то есть, его внутреннее устройство неизвестно. Мы смотрим, как он реагирует на входные сигналы, и стараемся подстроить модель так, чтобы выходы модели и объекта совпадали как можно точнее при разнообразных входах.

На практике часто используется смешанный способ: структура модели (вид уравнения, связывающего вход и выход) определяется из теории, а коэффициенты находят опытным путем. Например, общий вид уравнений движения корабля хорошо известен, однако в этих уравнениях есть коэффициенты, которые зависят от многих факторов (формы корпуса, шероховатости поверхности и т.п.), так что их крайне сложно (или невозможно) найти теоретически. В этом случае для определения неизвестных коэффициентов строят масштабные модели и испытывают их в бассейнах по специальным методикам. В авиастроении для тех же целей используют аэродинамические трубы.

Для любого объекта управления можно построить множество различных моделей, которые будут учитывать (или не учитывать) те или иные факторы.

Обычно используется компромиссный вариант. Начинают с простых моделей, стараясь спроектировать регулятор так, чтобы он «подходил» и для сложной модели. Затем проверяют работу построенного закона управления на полной модели или на реальном объекте. Если получен отрицательный результат (простой регулятор «не работает»), усложняют модель, вводя в нее дополнительные подробности.

Линеаризация.

Из курса математики известно, что проще всего решать линейные уравнения. С нелинейными уравнениями (квадратными, кубическими и др.) работать намного сложнее, многие типы уравнений математика пока не умеет решать аналитически (точно).

Однако, все модели реальных систем – нелинейные. Это легко понять хотя бы потому, что всегда есть предельно допустимое значение входного сигнала – при его превышении объект может просто выйти из строя или даже разрушиться (линейность нарушается). Методы исследования нелинейных операторов очень сложны математически, в теории нелинейных систем точные решения известны только для достаточно узкого круга задач. Во многих случаях более или менее точные модели представляют собой нелинейные дифференциальные уравнения, поэтому для того, чтобы применить теорию линейных систем, требуется линеаризация. Идея линеаризации заключается в том, что в системах регулирования сигналы мало отклоняются от рабочей точки – некоторого положения равновесия, в котором все сигналы имеют установившиеся значения и их производные равны нулю. Поэтому для решения задач управления часто достаточно использовать линейную модель в отклонениях от этой рабочей точки.

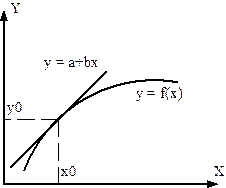
Дальше для линеаризации используется разложение функций в ряд Тейлора. Для некоторой функции f (x) в окрестности точки (x0) этот ряд имеет вид:

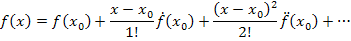
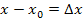
Рассмотрим САУ общем виде. Структура представлена на рис. 3.1.

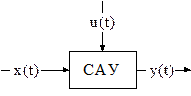
Рис. 3.1 Система автоматического управления.

Где Х(t) U(t) входные воздействия, а Y(t) – выходной параметр.

В общем виде функционирование непрерывной, линейной САУ описывается неоднородным дифференциальным уравнением следующего вида:

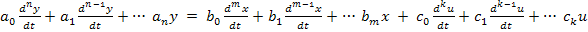(1)

Где: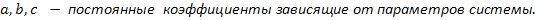

Введем оператор дифференцирования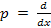

Тогда уравнение (1) может быть представлено в операторном виде:

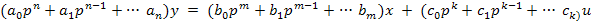(2)

В выражении (2) полином, стоящий при выходной переменной 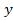называется собственным оператором и обозначается 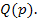Полиномы при входных параметрах 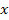и 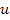называются соответственно оператором управляющего воздействия и оператором возмущающего воздействия и обозначаются 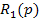и 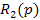, а уравнение (2) принимает вид:

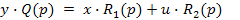(3)

Если рассматривать установившийся режим то уравнение (2) примет вид:

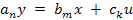(4)

Уравнение (2) описывает поведение САУ как в динамике, так и в статике, а уравнение (4) только в статике.

В тех случаях когда система или элемент описывается дифференциальным уравнением не выше второго порядка, используется стандартная система записи уравнения. Например , имеем САУ, которая содержит один вход 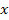и один выход 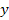, которая описывается уравнением

(5)

Левую и правую части уравнения (5) разделим на коэффициент :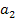

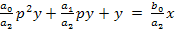(6)

Введем обозначения: , ,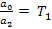

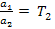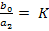
Тогда уравнение (6) принимает вид:

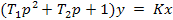(7)

В уравнении (7) параметр 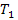имеет размерность 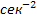, параметр 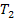имеет размерность 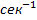, а параметр 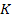безразмерный. Выражение (7) представляет собой уравнение в стандарной форме, которая наиболее удобна для дальнейшего анализа динамических процессов. В этом случае собственный оператор принимает вид алгебраического уравнения:

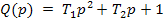(8)

Необходимо отметить, что оператор дифференцирования 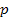имеет тесную связь с оператором интегрального преобразования Лапласа 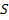, который является комплексною величиной. Как известно, для линейных дифференциальных уравнений с постоянными параметрами при нулевых начальных условиях и точностью до обозначения оператор 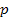соответствует оператору 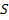, т.е. .

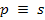Это обстоятельство позволяет использовать для решения уравнений типа (1) и для моделирования САУ интегральное преобразование Лапласа.

Напомним, что для преобразования функции действительной переменной 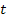на комплексной площади в функцию комплексной переменной 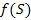используется выражение прямого преобразования Лапласа:

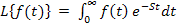(9)

Где: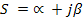

При этом функция 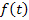называется оригиналом, а 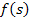изображением.

Функция 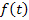имеет следующие особенности:

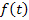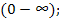
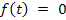- - определена и кусочно-дифференцируема на всей положительной числовой оси

- при .

- Существуют такие положительные числа 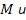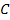, для которых выполняется соотношение:

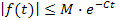при .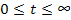

Переход от изображения 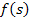к оригиналу 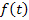(обратное преобразование Лапласа) выполняется следующим образом:

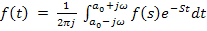(10)

Здесь интегрирование происходит вдоль любой прямой, которая удовлетворяет условиям 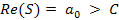. Символически обратное преобразование Лапласа обозначается в виде:

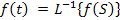(11)

3.3. Передаточные функции.

Понятие передаточная функция является наиболее важной категорией в теории автоматического управления и регулирования. Передаточная функция есть своего рода математической моделью САР, потому что полностью характеризует динамические параметры системы.

Передаточная функция представляет собой отношение изображения по Лапласу выходной величины 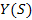к изображению входной величины , т.е. :

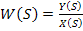(12)

Исходя и условия 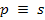для линейных систем уравнение (3) запишем в следующем виде:

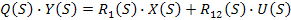(13)

Так как для линейных систем можно использовать принцип наложения, то возможно рассмотрение двух следующих случаев:

- сигнал 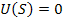, тогда ;

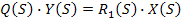- сигнал 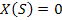, тогда ;

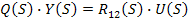Тогда, для любой САР, которая имеет входы управления и возмущения можно найти две передаточные функции:

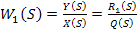(14)

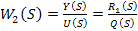(15)

Уравнение (14) является передаточной функцией по управлению, а выражение (15) передаточной функцией по возмущению.

Собственный оператор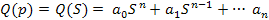

Соответственно оператор управляющего воздействия 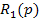и оператор возмущающего 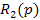выразим в таком же виде.

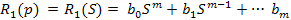
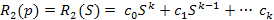
Следовательно, передаточные функции по управлению и по возмущающему воздействию будут представлять собой отношения следующих полиномов:

(16)

Для физической реализации необходимо чтобы выполнялись следующие условия 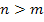и .

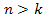Передаточные функции представляют особые точки на комплексной площади – нули и полюса. Полюса это те значения 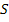, при которых передаточная функция стремится в бесконечность. Для определения полюсов необходимо собственный оператор (знаменатель передаточной функции) приравнять нулю и решить алгебраическое уравнение относительно 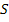. Нули – это такие значения 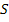, при который передаточная функция равняется нулю. Для определения нулей числитель передаточной функции приравнивается нулю и полученное алгебраическое уравнение решается относительно .

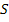Если задана структура САР, то можно определить передаточную функцию относительно любых двух точек структуры. При этом необходимо использовать существующие правила и методы структурных преобразований.