Гармоническое воздействие.

В условиях реальной эксплуатации САУ часто возникает необходимость определять реакцию на периодические сигналы, то есть определять сигнал на выходе САУ, если на один из входов подается периодический сигнал синусоидальной формы. Решение этой задачи можно получить путем использования частотных характеристик. Частотные характеристики могут быть получены экспериментальным и аналитическим путем. При аналитическом определении исходным моментом является одна из передаточных функций САУ (по управлению или по возмущению). Возможно также определение частотных характеристик, исходя из передаточных функций разомкнутой системы и передаточной функции по ошибке.

5.2 Частотная передаточная функция

Если на вход любой системы подать сигнал синусоидальной формы

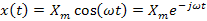
Очевидно, что выходной сигнал будет иметь ту же форму

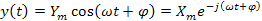
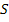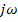Для нахождения соотношения между входными и выходными сигналами можно воспользоваться передаточной функцией, из которой формальной заменой на получаем обобщенную частотную характеристику

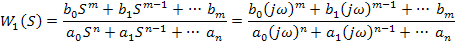
которая является комплексным выражением, то есть:

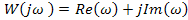
Где 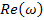действительная часть, а 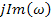- мнимая часть.

Частотная передаточная функция может быть представлена в показательной форме:

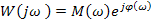
Где 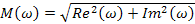модуль, а 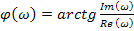– аргумент частотной передаточной функции.

Функция 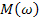, представлена при изменении частоты от 0 до бесконечности, получила название амплитудно-частотной характеристики (АЧХ).

Функция 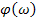, представленная при изменении частоты от 0 до бесконечности, называется фазово-частотной характеристикой (ФЧХ).

5.3 Амплитудно-фазовая частотная характеристика или годограф Найквиста (КЧХ)

Амплитудно-фазовая частотная характеристика или годограф Найквиста это графическое отображение для всего спектра частот отношения выходного сигнала САУ к входному сигналу в комплексной форме. Частотная передаточная функция 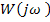может быть представлена на комплексной площади. В этом случае для каждой из частот в диапазоне от 0 до бесконечности происходит определение вектора на комплексной плоскости, и строиться годограф вектора. Годограф будет представлять собой амплитудно-фазово-частотную характеристику (АФЧХ). Таким образом, для определенной частоты мы имеем вектор на комплексной площади, который характеризуется модулем М 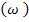и аргументом 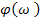. Модуль представляет собой численное отношение амплитуды выходного гармонического сигнала к амплитуде входного. Аргумент представляет собой сдвиг по фазе выходного сигнала относительного входного. При этом отрицательный фазовый сдвиг представляет вращение вектора на комплексной площади по часовой стрелке относительно положительной оси. А положительный фазовый сдвиг - против часовой стрелки. Пример такой характеристики показан на рисунке 4.2

Рисунок 4.2 график отображения амплитудно-фазовой характеристики АФХ или годографа Найквиста.

Из АФХ порождаются все остальные частотные зависимости:

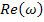– вещественная частотная характеристика

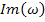– мнимая частотная характеристика

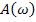– амплитудно-частотная характеристика АЧХ

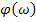– фазово-частотная характеристика ФЧХ

Наиболее часто применяются ЛАЧХ и ЛФЧХ.