Типовые динамические звенья. Общие характеристики.

Для решения задач анализа и синтеза линейных САУ целесообразно проводить их в виде соединения между собой несложных элементов с определенными динамическими характеристиками.

Разнообразие реальных элементов САУ сводится к небольшому числу так называемых типовых звеньев. Типовым элементарным звеном называется такое звено, которое невозможно разделить на ещё более простые звенья. Типовые звенья характеризуются следующими общими свойствами:

a) Имеют одну входную и одну выходную величины

b) Описываются дифференциальным уравнением не выше 2-го порядка.

c) Пропускают сигнал только в одном направлении.

По динамическим характеристикам типовые звенья делятся на следующие группы: позиционные, дифференцирующие и интегрирующие. У позиционных звеньев наблюдается линейная зависимость меду входными и выходными сигналами. В дифференцирующем звене выходной сигнал пропорциональный производной во времени от входного сигнала. В интегральном звене выходной сигнал пропорционален интегралу во времени входного сигнала.

Передаточную функцию любой САУ в общем виде можно представить как сумму передаточных функций вида:

Типовые динамические звенья

Обычно система управления состоит из отдельных блоков, каждый из которых описывается уравнениями низкого порядка (чаще всего – первого или второго). Для понимания работы

системы в целом желательно хорошо представлять, как ведут себя ее отдельные элементы.

Кроме того, при построении ЛАФЧХ сложной системы передаточную функцию разбивают на

простейшие сомножители

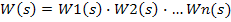
и далее, воспользовавшись свойствами ЛАФЧХ, строят характеристики для всей системы как

суммы ЛАЧХ и ЛФЧХ отдельных звеньев.

Усилитель

Звенья, имеющие конечный ненулевой коэффициент усиления постоянного сигнала, то

есть W(0) = k ≠ 0, называются позиционными. Это значит, что числитель и знаменатель переда-

точной функции имеют ненулевые свободные члены (постоянные слагаемые).

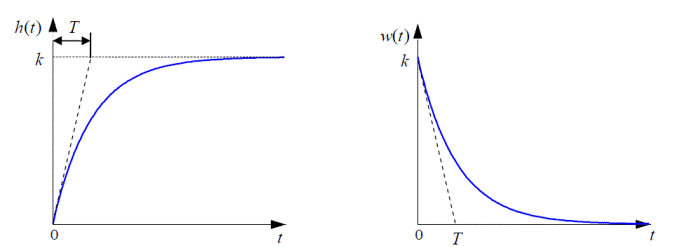
Простейшее позиционное звено – идеальный (безынерционный) усилитель. Его передаточная функция W(s) = k . Строго говоря, он не является динамическим звеном, поскольку изменение выхода происходит мгновенно, сразу вслед за изменением входа. При действии на вход единичного ступенчатого сигнала 1(t) (или дельта-функции δ (t) ) на выходе будет такой же сигнал, усиленный в k раз, поэтому переходная и импульсная характеристики звена равны

h(t) = k (t > 0) и w(t) = k ⋅δ (t) .

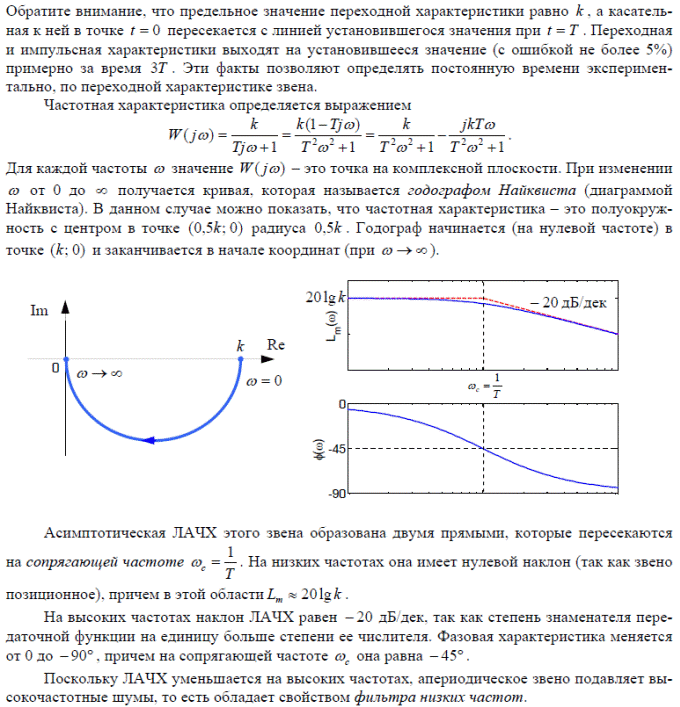
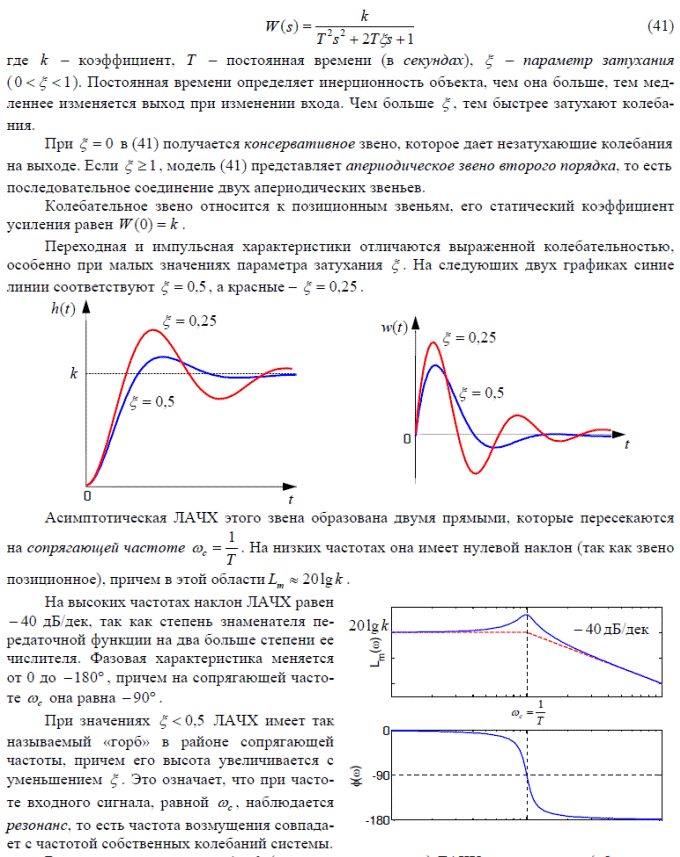
Если на вход усилителя действует синусоидальный сигнал, на выходе он усиливается в k раз без изменения фазы, поэтому амплитудная и фазовая частотная характеристики не зависят от частоты входного сигнала: A(ω) = k , φ (ω) = 0 .

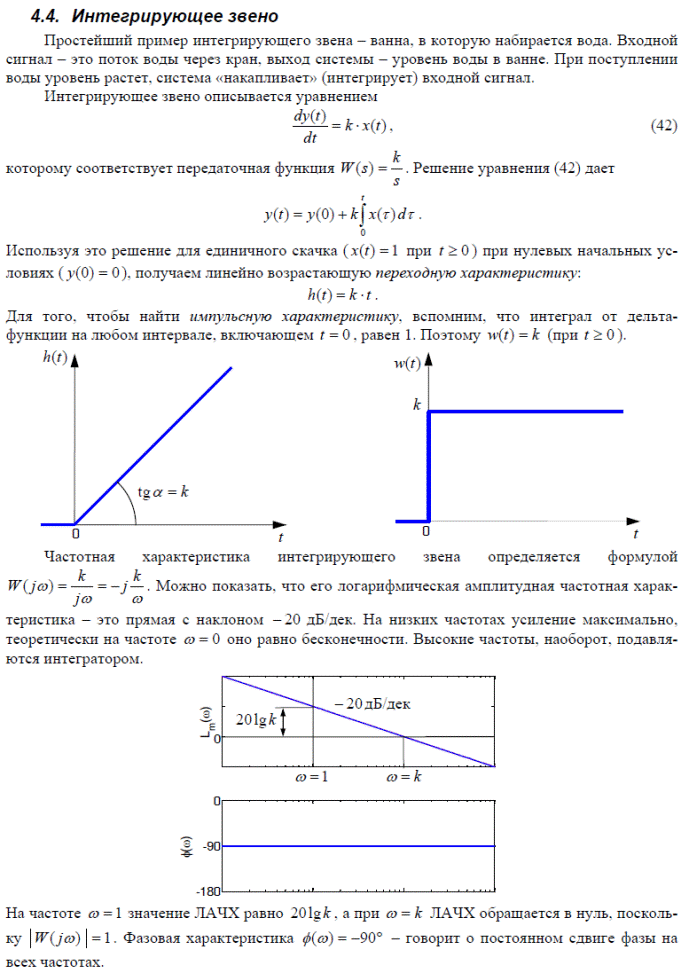
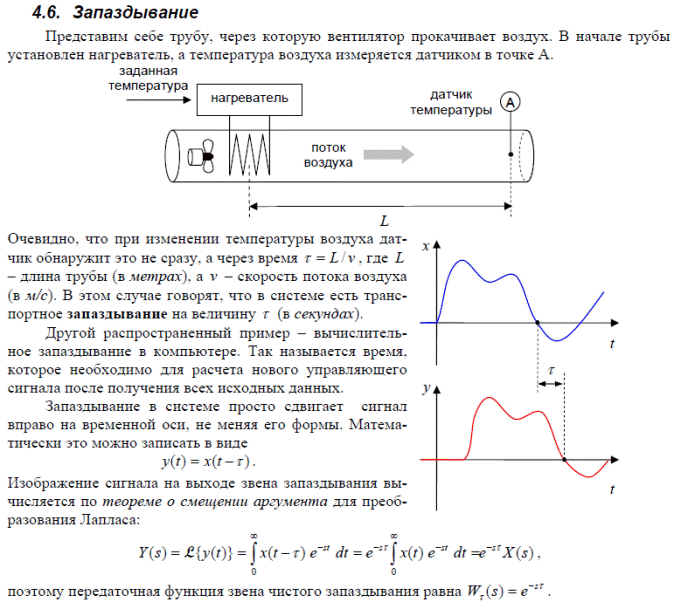
Устойчивость систем автоматического управления и методы её оценки.

Устойчивость – это свойство САУ возвращаться в состояния покоя или установившегося движения, из которого система была выведена каким-либо воздействием после устранения этого воздействия.

Обычно понятие устойчивости иллюстрируется следующими примерами. Будем считать системой некоторый шар, который может находиться в одном из трех состояний:

1)
если шар находится на вогнутой поверхности (рис. 3.1, а), то при наличии силы F, соответствующей внешнему воздействию на систему, шар можно вывести из состояния покоя. Если теперь устранить воздействие F, то шар после совершения нескольких колебаний около точки равновесия А придет в установившееся состояние (или состояние покоя), соответствующее точке А. Это пример устойчивого равновесия – система является устойчивой;

2) если к шару, находящемуся на выпуклой поверхности (рис. 3.1, б), приложена сила F, то, отклонившись под воздействием этой силы в точку B, шар после прекращения воздействия силы не придет в установившееся положение (в точку А). Такое состояние является неустойчивым;

3) если шар находится на шероховатой ровной поверхности (рис. 3.1, в) и к нему приложена сила F, то шар выйдет из состояния равновесия и после снятия воздействия придет в новое состояние равновесия. В зависимости от величины и знака силы F шар может иметь бесчисленное множество точек равновесия. Такое состояние носит название нейтрально-устойчивого, т.е. система является нейтрально-устойчивой.