Квадратичный критерий

.

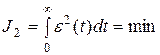J₂ тем меньше, чем меньше t_рег; меньше перерегулирование s; чем ближе h(t) к 1(t).

− большая величина J₂ может соответствовать более плавному апериодическому процессу, по сравнению с более быстрым, но колебательным процессом. То есть квадратичный критерий J₂ не дает представления о характере переходного процесса (колебательный или монотонный).

Учитывая эти недостатки J_2, был предложен обобщенный интегральный критерий

,

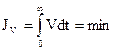где .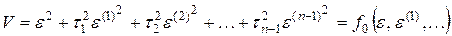

Суть минимизации этого критерия в том, что запрещаются большие отклонения как координаты e, так и ее производных. Поэтому при минимизации 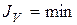должны получаться процессы быстрее и без значительных колебаний.

Обобщенный интегральный критерий J_V получил большое распространение при косвенной оценке качества переходного процесса.

Рассмотрим условия минимизации функционалов качества.

Квадратичный критерий.

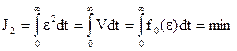
Уравнение Эйлера определяет необходимое условие экстремума функционала

.

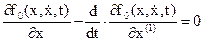То есть экстремум функционала J_V имеет место на экстремалях, которыми являются решения уравнения Эйлера, то есть решениях этого уравнения.

Имеем для 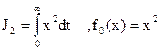, здесь принято .

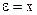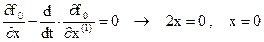
Это означает, что переменная x должна скачком измениться из положения x₀ до x=0. То есть процесс должен быть скачкообразным, а реальные системы все инерционные.

Обобщенный интегральный критерий.

.

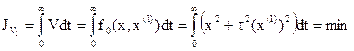
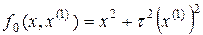Составляем уравнение Эйлера.

.

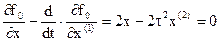Получилось дифференциальное уравнение второго порядка

.

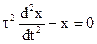Характеристическое уравнение для него

.

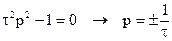Решение уравнения Эйлера принимает вид

.

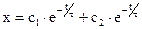Постоянная интегрирования c₂=0, так как по замыслу 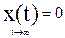, то есть система должна быть устойчивой.

Окончательно решение уравнения Эйлера имеет вид

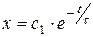, при t=0 находим 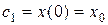, то есть имеем .

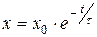Таким образом, экстремалью для функционала 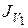будет экспонента.

Для разных t получим поле экстремалей, из них нужно выбрать одну, которая наиболее полно отвечает системе.

Рассмотрим более сложный обобщенный критерий

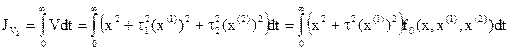
Для нахождения экстремали функционала 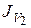составляем уравнение Эйлера-Пуассона

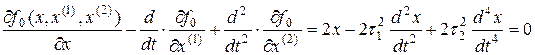
Получаем дифференциальное уравнение четвертого порядка

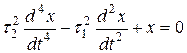
Составляем характеристическое уравнение

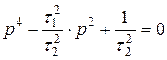
Решая это уравнение, получим четыре корня p₁–p₄, два из них p₁, p₂ с отрицательными вещественными частями, два других p₃, p₄ с положительными вещественными частями.

Так как система должна быть устойчивой, то будим учитывать только корни p₁, p₂ с отрицательными вещественными частями. В этом случае решение уравнения Эйлера будет иметь вид

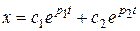
Из начальных условий при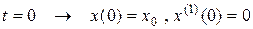

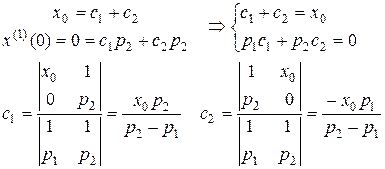
Решение уравнения Эйлера-Пуассона окончательно принимает вид

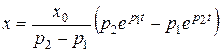
Таким образом, экстремалью для функционала 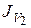является решение дифференциального уравнения второго порядка. Любая другая кривая не будет экстремалью и значение интеграла не будет минимальным. Корни p₁, p₂ могут быть и комплексно-сопряженными, поэтому в этом случае экстремаль будет носить колебательный характер.

Для более сложной обобщенной интегральной оценки

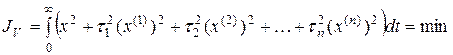
экстремалью будет решение дифференциального уравнения n-го порядка

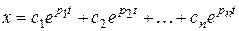, если все корни p_i – левые.

Следует отметить, что нельзя дать универсального критерия оптимальности, пригодного для всех видов систем управления, в каждом конкретном случае необходимо учитывать особенности систем и подбирать для нее соответствующий критерий, который бы наиболее полно учитывал особенности этой системы.

2. Аналитическое конструирование регуляторов с помощью принципа максимума по квадратичным критериям качества

Пусть объект управления описывается уравнением

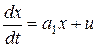
Краевые условия

.

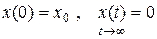Ограничение на управление

.

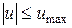Критерий качества

.

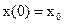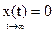Требуется перевести объект управления из в при минимизации критерия качества 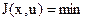с учетом ограничения на управление.

Согласно принципу максимума вводится дополнительная переменная

.

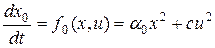Поэтому переходим к системе уравнений

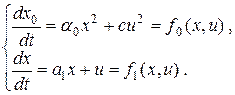
Функция Гамильтона имеет вид

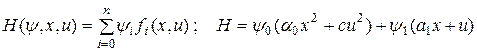
Сопряженная система дифференциальных уравнений для вспомогательных переменных имеет вид

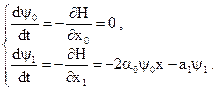
Далее находим .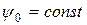

Из выражения для функции Гамильтона рассмотрим лишь члены, зависящие от управления u.

.

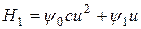Максимумы H и H₁ по управлению u будут совпадать, считая y₀=-1, получаем

.

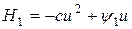Найдем экстремум H₁ по управлению u

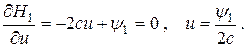
Таким образом, оптимальное управление определяется так

(*)

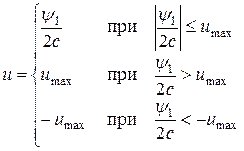Далее, выразим управление u через выходную переменную x. Для этого необходимо найти связь между вспомогательной переменной y₁, через которую представлен закон управления (*), и выходной переменной x.

Учитывая, что для экстремали найдено 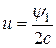, рассмотрим уравнения

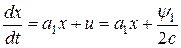– исходное уравнение

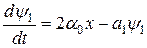– сопряженное уравнение

Решая эту систему уравнений, необходимо переменную y₁ выразить через x. Но здесь также начальные условия для x заданы, а для y₁ – неизвестны.

Найдем решение для этой системы уравнений. Удобнее перейти к операторной форме записи

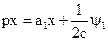
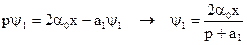
Характеристическое уравнение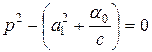

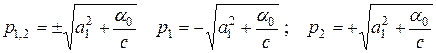
Решение для 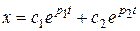, получаем .

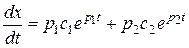Подставляем 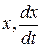в уравнение 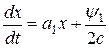, получаем 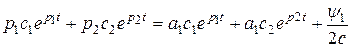, отсюда для y₁ находим .

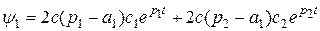Таким образом, получаем решения для x и y₁.

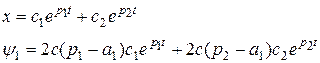
Для устойчивой системы необходимо положить c₂=0, в противном случае при t®¥, x®¥.

При c₂=0 . Исключая 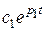находим .

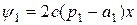Таким образом, закон управления через x принимает вид

Имели:Получили:

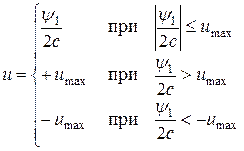
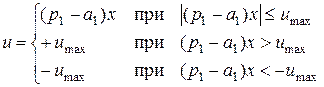
где .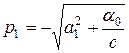

3. Аналитическое конструирование регуляторов по критерию обобщенной работы

Функционал качества общего вида в форме задачи Больца записывается так

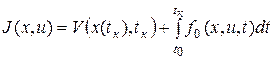
Эта общая формула функционала, которую называют классической. Минимизация этого функционала при оптимизации многомерных, нелинейных систем связана с большими трудностями. Поэтому часто пытаются упростить это выражение.

Подынтегральная функция f₀(x,u,t) зависит от двух векторных аргументов: вектора состояния x и вектора управления u, что в основном и является причиной возникающих трудностей при решении задачи оптимизации.

Решение упрощается, если функцию f₀(x,u,t) можно представить в виде суммы функций, зависящих только от x(t), t и от u(t), t то есть

,

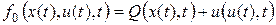где Q и u – заданные, обычно положительные функции.